 por epicfail » Seg Fev 07, 2011 16:49
por epicfail » Seg Fev 07, 2011 16:49
Estou travado há 5 dias. Não consegui encontrar ninguém para me ajudar até agora. O dúvida surgiu enquanto eu resolvia alguns exercícios do Caderno da turma ITA Poliedro. Exercícios de revisão de álgebra elementar.
Trabalhando com várias incognitas, x, m, p, os exercicios pedem para achar os valores que tornam a equação impossivel, outros para que a equação nao tenha solução.
o que encontrei foi pra IMPOSSIVEL x = -x
MAS para a equação SEM SOLUÇÃO x - x = 5 + p, tal que p diferente de -5
Por que ? Se é impossivel, consequentemente não tem solução, ou eu tou errado ? Por que p tem que ser diferente de -5 ? Por que nao posso zerar ?
1) m²x - m² = 2m + 2mx, R.:2. Valor de m que torna equação impossível.
4x - 4 = 4 + 4x
(m é igual a 2, substitui 2 em m, não em -m. Mas se eu substituisse em -m²)
4x + 4 = 4 + 4x
0 = 0
2) (2m-1).x = 3p -x - 2, R.: m = 0 e p diferente 2/3. Valor de m e p que tornam a equação sem solução.
- x = 6 - x - 2
0 = 4(qualquer valor diferente de 2/3), equação sem solução, mas não impossível
caso p 2/3
0 = 0, equação impossível, mas sem solução(?)
Por favor, se alguém puder esclarecer estas dúvidas ficarei grato.
-
epicfail
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 07, 2011 16:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Ter Fev 08, 2011 09:53
por DanielFerreira » Ter Fev 08, 2011 09:53
1) m²x - m² = 2m + 2mx, R.:2. Valor de m que torna equação impossível.
4x - 4 = 4 + 4x
(m é igual a 2, substitui 2 em m, não em -m. Mas se eu substituisse em -m²)
4x + 4 = 4 + 4x
0 = 0

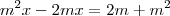
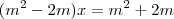


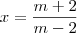 Epicfail
Epicfail,
para que a eq. seja impossível, deverá igualar seu denominador a zero.
daí,
m - 2 = 0
m = 2"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Ter Fev 08, 2011 09:59
por DanielFerreira » Ter Fev 08, 2011 09:59
2) (2m-1).x = 3p -x - 2, R.: m = 0 e p diferente 2/3. Valor de m e p que tornam a equação sem solução.
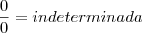
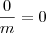
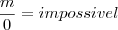



Se uma eq. não tem solução, ela é impossível:
2m = 0
m = 0Assim como na questão anterior, seu numerador é diferente (#) de zero.
3p - 2 # 0
p # 2/3"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por epicfail » Qui Fev 10, 2011 18:08
por epicfail » Qui Fev 10, 2011 18:08
Muito obrigado, danjr5.
-
epicfail
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 07, 2011 16:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sex Fev 11, 2011 15:09
por DanielFerreira » Sex Fev 11, 2011 15:09
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função de Primeiro Grau
por Najyh » Seg Mai 03, 2010 23:22
- 3 Respostas
- 5029 Exibições
- Última mensagem por MarceloFantini

Ter Mai 04, 2010 22:41
Funções
-
- Equação do primeiro grau
por isaiaspereira » Qui Jan 27, 2011 00:53
- 3 Respostas
- 2887 Exibições
- Última mensagem por Elcioschin

Qui Jan 27, 2011 14:02
Álgebra Elementar
-
- função do primeiro grau
por Abelardo » Qua Abr 27, 2011 19:35
- 2 Respostas
- 4186 Exibições
- Última mensagem por Abelardo

Qui Abr 28, 2011 11:08
Álgebra Elementar
-
- Função do Primeiro Grau
por Rafael16 » Sex Jan 11, 2013 21:20
- 2 Respostas
- 4107 Exibições
- Última mensagem por DanielFerreira

Sex Jan 11, 2013 22:27
Funções
-
- Equação do primeiro grau
por Netu » Sáb Jan 19, 2013 20:20
- 1 Respostas
- 1495 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 19, 2013 20:41
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



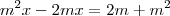
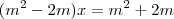


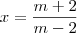

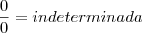
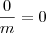
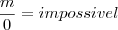




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.