 por Cristina Alves » Sex Fev 04, 2011 14:40
por Cristina Alves » Sex Fev 04, 2011 14:40
Olá estou com dúvida em uma questão parecida com a pergunta de Daniel (que esta postada no fórum como Moeda viciada) entendi o problema dele, mas não consigo resolver a minha questão.
Pergunta: Em uma moeda viciada, a probabilidade de sair CARA em um lançamento é quatro vezes maior do que a probabilidade de sair COROA. Ao final de três lançamentos dessa moeda, a probabilidade de obtermos, em qualquer ordem, duas COROAS e uma Cara é:
a) 3/8
b) 48/125
c) 12/125
d) 7/8
e) 3/4
Tentei assim: Duas Coroas e uma casa {ccc,cck,ckc,ckk,kkk,kcc,kkc,kck} = 3/8
P(CA) = 4 * P(CO)
P(CA) + P(CO) = 1
Mas não entendo os três lançamentos e nem moeda viciada, estou confusa e não consigo terminar o problema e chegar na resposta: (C) 12/125
-
Cristina Alves
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Fev 03, 2011 21:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por MarceloFantini » Sex Fev 04, 2011 17:24
por MarceloFantini » Sex Fev 04, 2011 17:24
Você estava no caminho certo. Veja:

Probabilidade de sairem duas coroas e uma cara, em UM dos casos:
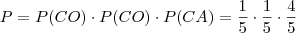
Como ele quer em QUALQUER ordem, devemos multiplicar por 3:
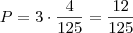
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cristina Alves » Sex Fev 04, 2011 21:37
por Cristina Alves » Sex Fev 04, 2011 21:37
Valeu Fantini...agora entendi, como é simples quando alguém nos ajuda!!! Decide estudar um pouco mais alguns exercícios que não domino muito e também provas de concurso, mas ando tendo muita dificuldade em alguns exercícios....obrigado pela ajuda!!!
-
Cristina Alves
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Fev 03, 2011 21:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidade ( Moeda Viciada)
por DanielRJ » Ter Set 21, 2010 17:53
- 2 Respostas
- 18885 Exibições
- Última mensagem por DanielRJ

Ter Set 21, 2010 19:25
Estatística
-
- 18)Probabilidade e Estatística - Uma moeda e um dado...?
por Hellsius » Dom Abr 24, 2011 16:33
- 1 Respostas
- 1857 Exibições
- Última mensagem por NMiguel

Dom Abr 24, 2011 17:13
Estatística
-
- [probabilidade lançamento moeda] Ajuda na questão!
por Andersonvrum » Ter Ago 02, 2011 12:45
- 4 Respostas
- 4197 Exibições
- Última mensagem por Andersonvrum

Seg Ago 08, 2011 15:30
Estatística
-
- [Probabilidade] peças dentro do padrão em três lotes
por leandrocf » Sex Jul 15, 2016 12:56
- 0 Respostas
- 3239 Exibições
- Última mensagem por leandrocf

Sex Jul 15, 2016 12:56
Probabilidade
-
- Três movimentos
por admin » Sáb Jul 21, 2007 01:16
- 2 Respostas
- 1908 Exibições
- Última mensagem por Neperiano

Seg Fev 09, 2009 10:36
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



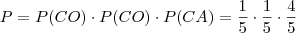
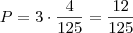



 .
.



