

bom eu tentei fazer por varias maneiras mais nao cheguei ao resultado certo.
ah deu certo por soma e produto , mais eu gostaria de saber como faz por
bhaskara.
obrigado por vc me ajudarem .




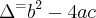
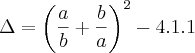

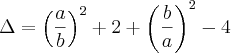

![\Delta=\sqrt[]{\left(\frac{a}{b} \right)^2+\left( \frac{b}{a}\right)^2 -2} \Delta=\sqrt[]{\left(\frac{a}{b} \right)^2+\left( \frac{b}{a}\right)^2 -2}](/latexrender/pictures/b99ff1aae829d202b17b64da004c9bdf.png)
![\Delta=\left(\frac{a}{b} \right)+\left( \frac{b}{a}\right)\sqrt[]{-2} \Delta=\left(\frac{a}{b} \right)+\left( \frac{b}{a}\right)\sqrt[]{-2}](/latexrender/pictures/a50bbe8f6e2f9548e35876aba21b8a6c.png)


 de k...
de k...
![\Delta=k^2-4
\Delta=\sqrt[]{k^2-4}
\Delta=k-2 \Delta=k^2-4
\Delta=\sqrt[]{k^2-4}
\Delta=k-2](/latexrender/pictures/f79090e359d7ef24fe3dcbe98d4eb927.png)
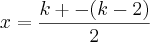

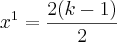
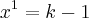

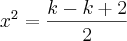








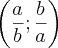





stanley tiago escreveu:dê o conjunto verdade da equaçao
mano nao é nada de mais , é materia da 8° serie equaçaozinha o 2° grau
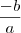 e o produto é igual a
e o produto é igual a  , então teremos:
, então teremos: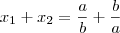
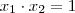

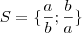


stanley tiago escreveu:sim renato . mais o caso é q eu ja tinha chegado nesse resultado , por soma e produto .
mais o caso em questao é q eu quero saber como faz por bhaskara .
foi o q eu tinha postado no primeiro post .
mais se nao for necessario pode deixar pra lá !




Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)