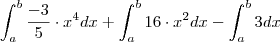Amigão, infelizmente não dá para saber qual é o limite inferior (me parece um 3), por isso farei a integral usando como limite inferior "a" e limite superior "b", então basta substituir, ok ?!
Vamos lá...

A integral da soma, é a soma das integrais, logo:
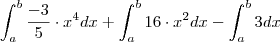
Colocando as constantes para fora da integral teremos:

Agora podemos resolver as integrais:

Aplicando os limites, teremos:

Agora basta substituir a e b pelos seus valores e fazer as contas...
Espero ter ajudado.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...