 por wandersonwfs » Qua Jan 19, 2011 23:08
por wandersonwfs » Qua Jan 19, 2011 23:08
boa noite
tem uma prova de matematica e não consegui resolver uma questao, esta questao estou enviando em anexo se alguem puder me ajudar fico grato...
obrigado
- Anexos
-

-
wandersonwfs
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jan 19, 2011 22:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: analise e desenvolvimento de sistemas
- Andamento: cursando
 por Elcioschin » Qui Jan 20, 2011 11:33
por Elcioschin » Qui Jan 20, 2011 11:33
Não dá para ler tudo.
Porque você não digita?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por wandersonwfs » Qui Jan 20, 2011 13:14
por wandersonwfs » Qui Jan 20, 2011 13:14
Boa Tarde,
Eu so preciso resolver esta questão nro 3
-
wandersonwfs
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jan 19, 2011 22:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: analise e desenvolvimento de sistemas
- Andamento: cursando
 por Renato_RJ » Qui Jan 20, 2011 14:53
por Renato_RJ » Qui Jan 20, 2011 14:53
Amigão, infelizmente não dá para saber qual é o limite inferior (me parece um 3), por isso farei a integral usando como limite inferior "a" e limite superior "b", então basta substituir, ok ?!
Vamos lá...

A integral da soma, é a soma das integrais, logo:
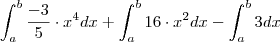
Colocando as constantes para fora da integral teremos:

Agora podemos resolver as integrais:

Aplicando os limites, teremos:

Agora basta substituir a e b pelos seus valores e fazer as contas...
Espero ter ajudado.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por wandersonwfs » Qui Jan 20, 2011 18:27
por wandersonwfs » Qui Jan 20, 2011 18:27
Boa boite Renato,
Imprimir o resultado que voce me passaou para terminar de resolver mas não estou conseguingo, voce pode fazer por mim.
Fiquei 15 anos longe da escola e agora que voltei para faculdade me aparece um problemão deste ai fiquei doido.
-
wandersonwfs
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jan 19, 2011 22:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: analise e desenvolvimento de sistemas
- Andamento: cursando
 por Renato_RJ » Qui Jan 20, 2011 20:50
por Renato_RJ » Qui Jan 20, 2011 20:50
Boa noite Wander...
Eu já te dei a resposta, basta colocar o 8 onde está a letra b e o limite inferior (que eu não consigo ler na foto) no lugar da letra a e fazer as contas...
Se, mesmo assim, ainda tiver problemas, posta quais são os limites da integral.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- prova da puc
por cleversonluizv » Qui Mar 14, 2013 15:23
- 1 Respostas
- 1381 Exibições
- Última mensagem por young_jedi

Sex Mar 15, 2013 11:36
Análise Combinatória
-
- [prova]
por Ge_dutra » Qui Mar 21, 2013 22:51
- 2 Respostas
- 1449 Exibições
- Última mensagem por Ge_dutra

Sex Mar 22, 2013 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Prova 1 - 2002
 por admin » Sáb Jul 21, 2007 05:53
por admin » Sáb Jul 21, 2007 05:53
- 0 Respostas
- 1497 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:53
Cálculo Numérico e Aplicações
-
- Prova 1 - 2004
 por admin » Sáb Jul 21, 2007 05:55
por admin » Sáb Jul 21, 2007 05:55
- 0 Respostas
- 1598 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:55
Cálculo Numérico e Aplicações
-
- Prova 2 - 2004
 por admin » Sáb Jul 21, 2007 05:56
por admin » Sáb Jul 21, 2007 05:56
- 0 Respostas
- 1563 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:56
Cálculo Numérico e Aplicações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






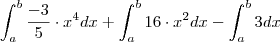






 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
