 por felipe170480 » Dom Jan 16, 2011 17:24
por felipe170480 » Dom Jan 16, 2011 17:24
gostaria de uma ajuda, preciso da formula de calculo de uma figura q nao sei o nome...bom seria um cilindro conico, vou postar a imagem do q seria e conto com a ajuda de vcs mto obrigado
- Anexos
-

- segue a imagem com detalhes da figura
-
felipe170480
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jan 16, 2011 16:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por felipe170480 » Dom Jan 16, 2011 17:26
por felipe170480 » Dom Jan 16, 2011 17:26
opa soh corrigindo....nao seria raio e sim diametro...obrigado
-
felipe170480
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jan 16, 2011 16:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Dan » Dom Jan 16, 2011 17:39
por Dan » Dom Jan 16, 2011 17:39
Na verdade esse sólido deve ser pensado em duas partes: um cilindro e um tronco de cone.
O que você deseja calcular? Superfície ou volume?
De qualquer forma você encontra as fórmulas na internet. Basta procurar por cilindro e tronco de cone.
Caso você deseje calcular a superfície, não esqueça de descontar a base maior do tronco de cone e uma das bases do cilindro.
Qualquer dúvida é só falar.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por felipe170480 » Dom Jan 16, 2011 17:49
por felipe170480 » Dom Jan 16, 2011 17:49
Dan escreveu:Na verdade esse sólido deve ser pensado em duas partes: um cilindro e um tronco de cone.
O que você deseja calcular? Superfície ou volume?
De qualquer forma você encontra as fórmulas na internet. Basta procurar por cilindro e tronco de cone.
Caso você deseje calcular a superfície, não esqueça de descontar a base maior do tronco de cone e uma das bases do cilindro.
Qualquer dúvida é só falar.
caro amigo gostaria de calcular o volume, esta parte de baixo se chama tronco de cone eh isso? vou procurar mas se alguem ja tiver um link q pudesse postar ou a formula mesmo pq ja procurei mto e na verdade nao axo desta fig.
-
felipe170480
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jan 16, 2011 16:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Dan » Dom Jan 16, 2011 17:51
por Dan » Dom Jan 16, 2011 17:51
Como você quer o volume as fórmulas são:
Tronco de cone:
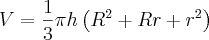
Onde h é a altura do tronco de cone, r é o raio da base menor e R é o raio da base maior.
Para calcular o volume do cilindro basta fazer área da base vezes altura.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Volume] Volume de caixa para carrinho de mão
 por MateusDantas1 » Seg Nov 05, 2012 20:12
por MateusDantas1 » Seg Nov 05, 2012 20:12
- 0 Respostas
- 2734 Exibições
- Última mensagem por MateusDantas1

Seg Nov 05, 2012 20:12
Geometria Espacial
-
- [Cálculo do Volume] Variação do volume em porcentagem
por Douglaasag » Sex Out 10, 2014 09:23
- 0 Respostas
- 4483 Exibições
- Última mensagem por Douglaasag

Sex Out 10, 2014 09:23
Cálculo: Limites, Derivadas e Integrais
-
- volume da planta de uma piscina [volume]
 por moraesfran » Ter Nov 15, 2011 21:38
por moraesfran » Ter Nov 15, 2011 21:38
- 0 Respostas
- 2096 Exibições
- Última mensagem por moraesfran

Ter Nov 15, 2011 21:38
Trigonometria
-
- Volume
por Pri Ferreira » Qua Mar 21, 2012 13:22
- 1 Respostas
- 1660 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 18:46
Geometria Espacial
-
- volume
por acalves » Sáb Abr 07, 2012 01:39
- 2 Respostas
- 1854 Exibições
- Última mensagem por Guill

Dom Abr 08, 2012 15:47
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






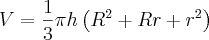

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.