 por saimonjhanna » Qua Jan 12, 2011 15:05
por saimonjhanna » Qua Jan 12, 2011 15:05
Urgente.. construa a matriz A=(aij)3x3, tal que?
tal que:
aij= { (-1)i+j, se i

j
aij= {
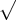
2, se i=j
Obrigado desde Já..
-
saimonjhanna
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jan 11, 2011 15:11
- Formação Escolar: SUPLETIVO
- Andamento: cursando
 por Molina » Qua Jan 12, 2011 16:48
por Molina » Qua Jan 12, 2011 16:48
saimonjhanna escreveu:Urgente.. construa a matriz A=(aij)3x3, tal que?
tal que:
aij= { (-1)i+j, se i

j
aij= {
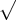
2, se i=j
Obrigado desde Já..
Boa tarde.
Primeiramente construa uma matriz dessa forma:

Agora basta ver os índices das entradas e fazer a alteração que o enunciado pede. Lembrando sempre que o primeiro número do índice refere-se ao
i e o segundo número do índice refere-se ao
j.
Por exemplo, o primeiro elemento, que é o

tem

, então no lugar deste elemento você vai colocar

.
Faça isso com os outros elementos.
Qualquer dúvida, informe!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Combinação Linear] com Matrizes, URGENTE!!!
por cotonete » Dom Jan 22, 2012 23:34
- 2 Respostas
- 2251 Exibições
- Última mensagem por cotonete

Seg Jan 23, 2012 21:50
Matrizes e Determinantes
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5157 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3603 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 6002 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9693 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 j
j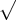 2, se i=j
2, se i=j
 j
j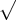 2, se i=j
2, se i=j
j
2, se i=j

 tem
tem  , então no lugar deste elemento você vai colocar
, então no lugar deste elemento você vai colocar  .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.