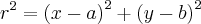
em que (a,b) é o centro da circunferência.
Questão:
Dada uma circunferência no plano, com raio igual a 3 e um ponto P pertencente à circunferência de coordenadas
 , calcule o par ordenado correspondende ao centro da circunferência.
, calcule o par ordenado correspondende ao centro da circunferência.Eu ainda comecei por aplicar a equação, mas perante duas variáveis ( a e b), concluí rapidamente que existem inúmeras soluções.
Existe um número ilimitado de circunferências, que tendo r=3, passam pelo ponto P.
Estarei correcto?





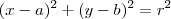 , onde (a ; b) representa as coordenadas do centro dessa circunferência.
, onde (a ; b) representa as coordenadas do centro dessa circunferência. , que pertencem à circunferência:
, que pertencem à circunferência: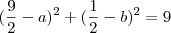
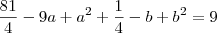

![b = \frac{-1 + \sqrt[]{117}}{2} b = \frac{-1 + \sqrt[]{117}}{2}](/latexrender/pictures/b3d22a058bb3047a28e5d9711cff4d7b.png)
![b = \frac{-1 - \sqrt[]{117}}{2} b = \frac{-1 - \sqrt[]{117}}{2}](/latexrender/pictures/eba4ae7a8dd441ef7443a4f547f96a5c.png)


 .
.
 :
: