 por gustavoluiss » Dom Jan 09, 2011 00:20
por gustavoluiss » Dom Jan 09, 2011 00:20
Não intendi nada dessa questão de função composta,alguém pode me ajudar ?


AI RENATO VE SE ME AJUDA VLW .
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Renato_RJ » Dom Jan 09, 2011 01:11
por Renato_RJ » Dom Jan 09, 2011 01:11
Salve grande Gustavo !!!
Seguinte meu amigo, repare que esse gráfico tem a seguinte propriedade:
f(x) =

se
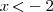
f(x) =

se
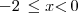
f(x) =

se
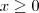
A equação

eu deduzi da reta crescente nos intervalos
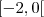
, então podemos deduzir o seguinte:
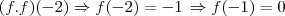
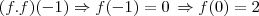
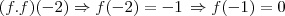
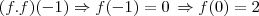
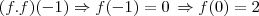
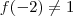
Logo, a resposta é a letra b.
Espero ter ajudado (e acertado.. rss..).
Renato.
Editado pela última vez por
Renato_RJ em Dom Jan 09, 2011 01:40, em um total de 1 vez.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por gustavoluiss » Dom Jan 09, 2011 01:20
por gustavoluiss » Dom Jan 09, 2011 01:20
po renato tu tah o bixo , é isso ai mesmo . vlw
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 se
se 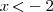
 se
se 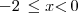
 se
se 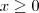
 eu deduzi da reta crescente nos intervalos
eu deduzi da reta crescente nos intervalos 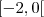 , então podemos deduzir o seguinte:
, então podemos deduzir o seguinte: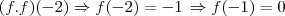
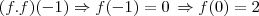
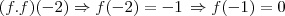
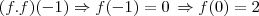
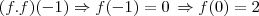




 , avisa que eu resolvo.
, avisa que eu resolvo.

