 por OtavioBonassi » Sex Jan 07, 2011 01:57
por OtavioBonassi » Sex Jan 07, 2011 01:57
Galera ,precisava calcular o seguinte limite levando em média no máximo 4 minutos , mas do jeito que eu to fazendo (L' Hopital) levaria uns 10 (pelo menos pra mim) !
O limite é o seguinte :
![\lim_{x\to_{-\infty}}\frac{\sqrt[2]{4x^2 + 7}}{\sqrt[3]{x^3+3x^2+1}} \lim_{x\to_{-\infty}}\frac{\sqrt[2]{4x^2 + 7}}{\sqrt[3]{x^3+3x^2+1}}](/latexrender/pictures/f20ebc39e321c651302164df9021cfec.png)
...
Conforme eu fui fazendo l' hopital foram aparecendo mais denominadores com raizes e ao invés de facilitar fui complicando !
Abraço,
Otávio
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Pedro123 » Sex Jan 07, 2011 02:02
por Pedro123 » Sex Jan 07, 2011 02:02
é meu caro, esse eu vou ficar te devendo, ainda não vi calculo... axo q vou começar a ver esse ano hsaushasuh
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por VtinxD » Sex Jan 07, 2011 12:35
por VtinxD » Sex Jan 07, 2011 12:35
Acho que se você transformar o limite para este limite fica mais facil de enxergar....
![\lim_{\infty}=\frac{\sqrt[6]{{(4{x}^{2}+7)}^{3}}}{\sqrt[6]{{({x}^{3}+3{x}^{2}+1)}^{2}}} \lim_{\infty}=\frac{\sqrt[6]{{(4{x}^{2}+7)}^{3}}}{\sqrt[6]{{({x}^{3}+3{x}^{2}+1)}^{2}}}](/latexrender/pictures/f0e5ccc1ad47bf5fb12fc4763b451631.png)
Agora ,eu acho,é só fazer a divisão de polinômios e analisar o polinômio do resto.Aparentemente você chega a esse polinômio:
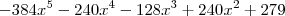
.Agora só usar as derivadas para descobrir , que ele só possui uma raiz real e quando x tende a -oo a função tende a +oo também.Você tambem pode perceber que -384x^5-128x^3+240x^2 cresce muito mais rapidamente que -240x^4 quando tendidos a numeros negativamente grandes ,tendendo assim para +oo.
Espero ter ajudado.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por OtavioBonassi » Sex Jan 07, 2011 16:14
por OtavioBonassi » Sex Jan 07, 2011 16:14
então nós temos um problema cara ,a resposta do exercicio é -2 hasuhsuahu
nao consegui chegar nela ,se analisarmos desse seu jeito a funçaõ tende a infinito mesmo, mas a resposta é -2 , tá ai o caô !
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por VtinxD » Sex Jan 07, 2011 16:56
por VtinxD » Sex Jan 07, 2011 16:56
Eh....O WolframAlpha diz que o limite é igual a
![1-\sqrt[]{3}i 1-\sqrt[]{3}i](/latexrender/pictures/e92b072d503cf2e7961c2025af97f522.png)
.Agora qual esta certo eu não sei dizer mas tenho quase certeza de que o meu anterior esta errado.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por OtavioBonassi » Sex Jan 07, 2011 17:00
por OtavioBonassi » Sex Jan 07, 2011 17:00
eix ,ai o wolfram já apelou ,meteu caiu no número imaginário ... esse exercício ai é um da fuvest ,e eles forneceram como gabarito o -2 mesmo ...
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Renato_RJ » Sex Jan 07, 2011 22:56
por Renato_RJ » Sex Jan 07, 2011 22:56
Colegas, usando a transformação sugerida pelo amigo VtinxD, teremos:
![\lim_{x\rightarrow\infty}{\frac{\sqrt[6]{(4*x^2+7)^3}}{\sqrt[6]{(x^3+3*x^2+1)^2}}} \lim_{x\rightarrow\infty}{\frac{\sqrt[6]{(4*x^2+7)^3}}{\sqrt[6]{(x^3+3*x^2+1)^2}}}](/latexrender/pictures/419dba74d814fe93a1594c8ae04e4b6f.png)
Desenvolvendo as potências teremos:
![\lim_{x\rightarrow\infty}{\sqrt[6]{\frac{64*x^6+336*x^4+588*x^2+343}{x^6+6*x^5+9*x^4+2*x^3+6*x^2+1}}} \lim_{x\rightarrow\infty}{\sqrt[6]{\frac{64*x^6+336*x^4+588*x^2+343}{x^6+6*x^5+9*x^4+2*x^3+6*x^2+1}}}](/latexrender/pictures/acc06e6670fffed0094bda6905898a1a.png)
Dividindo os termos por
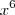
temos:
![\lim_{x\rightarrow\infty}{\sqrt[6]{\frac{(64+\frac{336}{x^2}+\frac{588}{x^4}+\frac{343}{x^6})}{(1+\frac{6}{x}+\frac{9}{x^2}+\frac{2}{x^3}+\frac{6}{x^4}+\frac{1}{x^6})}}} \lim_{x\rightarrow\infty}{\sqrt[6]{\frac{(64+\frac{336}{x^2}+\frac{588}{x^4}+\frac{343}{x^6})}{(1+\frac{6}{x}+\frac{9}{x^2}+\frac{2}{x^3}+\frac{6}{x^4}+\frac{1}{x^6})}}}](/latexrender/pictures/8d118446baed581474573fa2b9b2951d.png)
Aplicando o limite teremos:
![\sqrt[6]{64} \, \Rightarrow \sqrt[6]{2^6} \, \Rightarrow 2 \sqrt[6]{64} \, \Rightarrow \sqrt[6]{2^6} \, \Rightarrow 2](/latexrender/pictures/eed7efa8af20ed08b2bcf46cca6505ef.png)
Se cometi algum erro, por favor apontem, assim todos nós aprendemos...
Grato,
Renato.
P.S.: Correção quanto a raiz sêxtupla de 64, grato Fantini.
Editado pela última vez por
Renato_RJ em Sex Jan 07, 2011 23:47, em um total de 2 vezes.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por MarceloFantini » Sex Jan 07, 2011 23:32
por MarceloFantini » Sex Jan 07, 2011 23:32
Apenas uma correção no final:
![\sqrt[6]{64} = 2 \sqrt[6]{64} = 2](/latexrender/pictures/5d764e37b9fdb3722192b6ee8bfc0fbc.png)
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por OtavioBonassi » Sáb Jan 08, 2011 00:00
por OtavioBonassi » Sáb Jan 08, 2011 00:00
mas então ,sei lá ... é um exercicio teste na verdade , nao sei se esse é o caminho mesmo ... se eu adotasse esse caminho de dividir os polinomios pelo maior x elevado desde o começo ?! tipo, eu teria um resultado como infinito pô ... Acho que eu ter dado a resposta influenciou um certo caminho , vamos ver se mais alguem tem alguma resolução .
E também achoq ue a resposta tem que ser só uma né ,e não + ou - 2 , se voce pensar num gráfico tendendo pela esquerda no infinito nao tem como ter 2 resposta (no caso + ou - 2) , se x tendensse a outro número tudo bem ,mas ele tem a infinito, pelo menos na minha cabeça nesse caso nao tem como um limite lateral tender a 2 números ,tem ?
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Renato_RJ » Sáb Jan 08, 2011 01:51
por Renato_RJ » Sáb Jan 08, 2011 01:51
Grande Otávio, eu não me senti tendenciado pela resposta que você já tinha postado (o -2), tanto que eu disse que seria 2 devido ao fato de termos a
![\sqrt[6]{64} \sqrt[6]{64}](/latexrender/pictures/3a376bbb046aaf386dfaf17513ee9f7c.png)
no fim do limite (mesmo que o limite tenha tendência pela esquerda ou direita), só que eu demorei um tempo bem considerado para resolver... O que aconteceu comigo, foi que segui da dica do colega VtinxD para colocar os dois polinômios em uma raiz de mesma potência (facilitando as contas).
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por OtavioBonassi » Sáb Jan 08, 2011 09:30
por OtavioBonassi » Sáb Jan 08, 2011 09:30
Fala ai Renato ,tudo bem cara ? Achei um pequeno problema na resolução ,acho que voce copiou o limite do VtinxD e agora que eu percebi que ele copiou errado ,nao é o x tendendo ao infinito ,é x tendendo a menos infinito, ou seja ,um número ao invés de extremamente alto ,extremamente baixo ! Então as divisões ao invés de dar 0 dariam infinito ,ficando raiz de
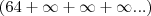
e assim vai . Agora ,nao sei se a raiz da soma de infinitos dividido pela raiz da soma dos infinitos é uma indeterminação ou não.
Acho que agora muda o rumo do exercício né ? haha
O x tende a
menos infinito.
Desculpe-me por nao ter percebido antes !
Abraços,
Otávio.
-
OtavioBonassi
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jan 05, 2011 14:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por Renato_RJ » Sáb Jan 08, 2011 12:15
por Renato_RJ » Sáb Jan 08, 2011 12:15
Fala Otavio, eu realmente copiei o limite do VtnixD, pois ele já tinha dado a sacada de colocar os dois polinômios com raízes de mesma potência, assim facilitou o meu raciocínio.. Quanto ao menos infinito, as frações tenderão ao zero, acho que ficamos na mesma...
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6644 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4790 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5119 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7258 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4435 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\to_{-\infty}}\frac{\sqrt[2]{4x^2 + 7}}{\sqrt[3]{x^3+3x^2+1}} \lim_{x\to_{-\infty}}\frac{\sqrt[2]{4x^2 + 7}}{\sqrt[3]{x^3+3x^2+1}}](/latexrender/pictures/f20ebc39e321c651302164df9021cfec.png)

![\lim_{x\to_{-\infty}}\frac{\sqrt[2]{4x^2 + 7}}{\sqrt[3]{x^3+3x^2+1}} \lim_{x\to_{-\infty}}\frac{\sqrt[2]{4x^2 + 7}}{\sqrt[3]{x^3+3x^2+1}}](/latexrender/pictures/f20ebc39e321c651302164df9021cfec.png)


![\lim_{\infty}=\frac{\sqrt[6]{{(4{x}^{2}+7)}^{3}}}{\sqrt[6]{{({x}^{3}+3{x}^{2}+1)}^{2}}} \lim_{\infty}=\frac{\sqrt[6]{{(4{x}^{2}+7)}^{3}}}{\sqrt[6]{{({x}^{3}+3{x}^{2}+1)}^{2}}}](/latexrender/pictures/f0e5ccc1ad47bf5fb12fc4763b451631.png)
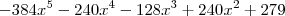 .Agora só usar as derivadas para descobrir , que ele só possui uma raiz real e quando x tende a -oo a função tende a +oo também.Você tambem pode perceber que -384x^5-128x^3+240x^2 cresce muito mais rapidamente que -240x^4 quando tendidos a numeros negativamente grandes ,tendendo assim para +oo.
.Agora só usar as derivadas para descobrir , que ele só possui uma raiz real e quando x tende a -oo a função tende a +oo também.Você tambem pode perceber que -384x^5-128x^3+240x^2 cresce muito mais rapidamente que -240x^4 quando tendidos a numeros negativamente grandes ,tendendo assim para +oo.

![1-\sqrt[]{3}i 1-\sqrt[]{3}i](/latexrender/pictures/e92b072d503cf2e7961c2025af97f522.png) .Agora qual esta certo eu não sei dizer mas tenho quase certeza de que o meu anterior esta errado.
.Agora qual esta certo eu não sei dizer mas tenho quase certeza de que o meu anterior esta errado.

![\lim_{x\rightarrow\infty}{\frac{\sqrt[6]{(4*x^2+7)^3}}{\sqrt[6]{(x^3+3*x^2+1)^2}}} \lim_{x\rightarrow\infty}{\frac{\sqrt[6]{(4*x^2+7)^3}}{\sqrt[6]{(x^3+3*x^2+1)^2}}}](/latexrender/pictures/419dba74d814fe93a1594c8ae04e4b6f.png)
![\lim_{x\rightarrow\infty}{\sqrt[6]{\frac{64*x^6+336*x^4+588*x^2+343}{x^6+6*x^5+9*x^4+2*x^3+6*x^2+1}}} \lim_{x\rightarrow\infty}{\sqrt[6]{\frac{64*x^6+336*x^4+588*x^2+343}{x^6+6*x^5+9*x^4+2*x^3+6*x^2+1}}}](/latexrender/pictures/acc06e6670fffed0094bda6905898a1a.png)
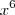 temos:
temos:![\lim_{x\rightarrow\infty}{\sqrt[6]{\frac{(64+\frac{336}{x^2}+\frac{588}{x^4}+\frac{343}{x^6})}{(1+\frac{6}{x}+\frac{9}{x^2}+\frac{2}{x^3}+\frac{6}{x^4}+\frac{1}{x^6})}}} \lim_{x\rightarrow\infty}{\sqrt[6]{\frac{(64+\frac{336}{x^2}+\frac{588}{x^4}+\frac{343}{x^6})}{(1+\frac{6}{x}+\frac{9}{x^2}+\frac{2}{x^3}+\frac{6}{x^4}+\frac{1}{x^6})}}}](/latexrender/pictures/8d118446baed581474573fa2b9b2951d.png)
![\sqrt[6]{64} \, \Rightarrow \sqrt[6]{2^6} \, \Rightarrow 2 \sqrt[6]{64} \, \Rightarrow \sqrt[6]{2^6} \, \Rightarrow 2](/latexrender/pictures/eed7efa8af20ed08b2bcf46cca6505ef.png)



![\sqrt[6]{64} \sqrt[6]{64}](/latexrender/pictures/3a376bbb046aaf386dfaf17513ee9f7c.png) no fim do limite (mesmo que o limite tenha tendência pela esquerda ou direita), só que eu demorei um tempo bem considerado para resolver... O que aconteceu comigo, foi que segui da dica do colega VtinxD para colocar os dois polinômios em uma raiz de mesma potência (facilitando as contas).
no fim do limite (mesmo que o limite tenha tendência pela esquerda ou direita), só que eu demorei um tempo bem considerado para resolver... O que aconteceu comigo, foi que segui da dica do colega VtinxD para colocar os dois polinômios em uma raiz de mesma potência (facilitando as contas).
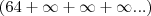 e assim vai . Agora ,nao sei se a raiz da soma de infinitos dividido pela raiz da soma dos infinitos é uma indeterminação ou não.
e assim vai . Agora ,nao sei se a raiz da soma de infinitos dividido pela raiz da soma dos infinitos é uma indeterminação ou não.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.