 por Raphael Feitas10 » Qua Jan 05, 2011 00:16
por Raphael Feitas10 » Qua Jan 05, 2011 00:16
Professor me tira essa duvida por favor
A soma de três mútiplos de 4 com quatro mútiplos de 3 e igual a 144.
Calcule o primeiro mútiplo desses numeros.
eu cheguei ate aqui depois ñ conseguei resolver mas
x+x+4+x+8+x+x+3+x+6+x+9=144
a reposta é 12
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por PedroSantos » Qua Jan 05, 2011 07:45
por PedroSantos » Qua Jan 05, 2011 07:45
Existe um número
x que é múltiplo comum de 3 e 4 de tal forma que
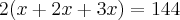
(multiplica-se por dois, porque se pede a soma dos multiplos de 3 e 4)

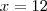
Intuitivamente bastava encontrar o M.M.C entre 3 e 4.
Dificil é:
A soma de três multiplos comuns entre 3 e 4 é igual a 108,qual é o menor de entre esses três?
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por Raphael Feitas10 » Qua Jan 05, 2011 12:54
por Raphael Feitas10 » Qua Jan 05, 2011 12:54
Ver se ta certo professor
2(x+2x+3x)=108
12x=108
x=108/12
x=9
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por PedroSantos » Qua Jan 05, 2011 19:49
por PedroSantos » Qua Jan 05, 2011 19:49
Se
x=9, então os outros multiplos serão 18 e 27. Todos eles são multiplos de 3, mas nenhum é multiplo de 4.
Julgo que a resolução deste tipo de problemas, passa por encontrar o MMC entre os dois números.Neste caso é o 12.
Seja
x um número inteiro positivo, 12
x será sempre um multiplo comum de 3 e 4.
Assim:

(só é pedido a soma dos múltiplos comun aos dois)




Se
x=2, então os três múltiplos são 24,36 e 48. O menor é o 24.
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números inteiros
por thadeu » Qui Nov 19, 2009 11:41
- 2 Respostas
- 2070 Exibições
- Última mensagem por thadeu

Qui Nov 19, 2009 13:46
Álgebra Elementar
-
- numeros inteiros
por edwilsoncrep » Qui Mar 04, 2010 20:03
- 5 Respostas
- 6390 Exibições
- Última mensagem por adriana_borges

Dom Mai 09, 2010 12:04
Sequências
-
- Numeros inteiros
por Raphael Feitas10 » Qui Jan 13, 2011 13:18
- 15 Respostas
- 9695 Exibições
- Última mensagem por Raphael Feitas10

Qua Jan 19, 2011 00:40
Números Complexos
-
- Numeros inteiros 2
por Raphael Feitas10 » Qua Jan 19, 2011 00:28
- 1 Respostas
- 2893 Exibições
- Última mensagem por Renato_RJ

Qua Jan 19, 2011 01:52
Funções
-
- Numeros inteiros 3
por Raphael Feitas10 » Qua Jan 19, 2011 17:03
- 1 Respostas
- 1661 Exibições
- Última mensagem por Molina

Qua Jan 19, 2011 21:49
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



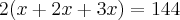 (multiplica-se por dois, porque se pede a soma dos multiplos de 3 e 4)
(multiplica-se por dois, porque se pede a soma dos multiplos de 3 e 4)
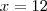


 (só é pedido a soma dos múltiplos comun aos dois)
(só é pedido a soma dos múltiplos comun aos dois)





 .
.



