 por Bruno Pinheiro » Ter Dez 28, 2010 01:12
por Bruno Pinheiro » Ter Dez 28, 2010 01:12
Estou com dúvidas no seguinte exercício. Segue abaixo o enunciado e minha proposta de solução:
(Gama Filho-RJ) O maior valor inteiro de x que é solução da inequação
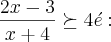
a) -8
b) -5 (gabarito)
c) -4
d) -3
e) +3
- minha resolução:
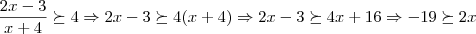
-
Bruno Pinheiro
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Dez 26, 2010 21:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por Molina » Ter Dez 28, 2010 12:51
por Molina » Ter Dez 28, 2010 12:51
Boa tarde, Bruno.
Também cheguei a mesma conclusão que você.
Deve ter algum erro na inequação, pois desta forma a resposta seria -9.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Jefferson » Qua Dez 29, 2010 00:56
por Jefferson » Qua Dez 29, 2010 00:56
Eu não sei porque, sempre se enganam ao responder questões com inequação.
O gabarito esta correto. Segue análise explicando o porque.
[O anexo não pode ser exibido, pois a extensão doc foi desativada pelo administrador.]
-
Jefferson
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Nov 16, 2010 23:18
- Localização: Vila Velha - ES
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Qua Dez 29, 2010 10:45
por MarceloFantini » Qua Dez 29, 2010 10:45
Jefferson, eu não olhei mas acredito que esteja correto, apenas recomendaria que das próximas vezes
evite colocar anexos e resolva as questões na forma de post.
Aqui vai a minha resolução (que deve ser igual/equivalente):
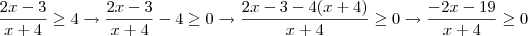
Para que isto seja atendido, devemos ter:
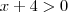
e

ou
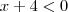
e

Logo:
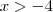
e
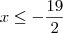
(impossível, pois não existe número que satisfaça)
ou
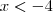
e
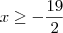
, de onde depreende-se de que o menor número inteiro que satisfaz isso é -5.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequação Quociente
por MERLAYNE » Qua Mai 09, 2012 11:08
- 2 Respostas
- 1652 Exibições
- Última mensagem por DanielFerreira

Qua Mai 09, 2012 22:48
Sistemas de Equações
-
- Inequação Quociente
por Luis_Hgl » Qua Fev 27, 2013 13:18
- 1 Respostas
- 3122 Exibições
- Última mensagem por young_jedi

Sex Mar 01, 2013 23:13
Inequações
-
- Inequação-quociente
 por Celma » Dom Jul 21, 2013 11:42
por Celma » Dom Jul 21, 2013 11:42
- 6 Respostas
- 3875 Exibições
- Última mensagem por Celma

Seg Jul 22, 2013 19:15
Inequações
-
- inequação produto/quociente
por vhcs29 » Qui Abr 01, 2010 12:32
- 2 Respostas
- 5300 Exibições
- Última mensagem por vhcs29

Sex Abr 02, 2010 12:59
Álgebra Elementar
-
- Inequação Quociente (Módulo)
por Rafael16 » Sex Jul 06, 2012 12:43
- 1 Respostas
- 2193 Exibições
- Última mensagem por Russman

Sex Jul 06, 2012 17:24
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
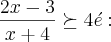
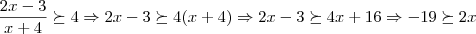

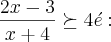
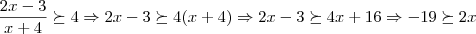




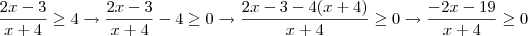
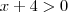 e
e 
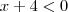 e
e 
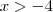 e
e 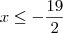 (impossível, pois não existe número que satisfaça)
(impossível, pois não existe número que satisfaça)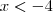 e
e 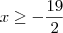 , de onde depreende-se de que o menor número inteiro que satisfaz isso é -5.
, de onde depreende-se de que o menor número inteiro que satisfaz isso é -5.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.