 por weverton » Dom Out 24, 2010 02:54
por weverton » Dom Out 24, 2010 02:54
1- quais são os valores que k pode assumir para que a equação x^2+y^2-2x+10y+13k=0 , represente uma circunferência?
obs:tentei fazer mais nao sei se ta certo, olhem os resultados q achei k=1,k=2,k=-1
me ajudem e me mostrem como chegaram ao resultado!
obrigado
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por weverton » Dom Out 31, 2010 02:18
por weverton » Dom Out 31, 2010 02:18
weverton escreveu:1- quais são os valores que k pode assumir para que a equação x^2+y^2-2x+10y+13k=0 , represente uma circunferência?
obs:tentei fazer mais nao sei se ta certo, olhem os resultados q achei k=1,k=2,k=-1
me ajudem e me mostrem como chegaram ao resultado!
obrigado
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por luispereira » Qui Dez 23, 2010 19:40
por luispereira » Qui Dez 23, 2010 19:40
A equação geral desta circunferência é:

como o termo da direita é iqual o raio ao quadrado, temos que cumprir a condição deste ser MAIOR que zero dado que senão, não haverá o círculo.
Daí:
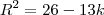
onde a porção da direita tem q ser maior q zero. Isso se da para valores de K maiores que 2 e para uma solução mais formal:
![k=]2,\infty[ k=]2,\infty[](/latexrender/pictures/77f37cec0c32678a1b303efc44947fbd.png)
-
luispereira
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Dez 23, 2010 18:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Sex Dez 24, 2010 18:16
por Elcioschin » Sex Dez 24, 2010 18:16
Houve um pequeno erro no final:
26 - 13k > 0
13k < 26
k < 2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quais os possíveis valores que satisfazem os valores reais
por andersontricordiano » Seg Fev 24, 2014 22:53
- 1 Respostas
- 5154 Exibições
- Última mensagem por Russman

Ter Fev 25, 2014 02:17
Números Complexos
-
- Quais os subconjuntos de A={a,{b,c},D}?
por vitor lima » Seg Mar 15, 2010 21:49
- 5 Respostas
- 3290 Exibições
- Última mensagem por Molina

Ter Mar 16, 2010 22:04
Conjuntos
-
- Quais os números que são as raízes do seguinte polinômio
por andersontricordiano » Sáb Fev 25, 2012 01:22
- 1 Respostas
- 1607 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:51
Polinômios
-
- [Vetores - teoria] Quais afirmações são verdadeiras?
por manoelcarlos » Seg Set 30, 2013 23:51
- 1 Respostas
- 998 Exibições
- Última mensagem por Russman

Qua Out 02, 2013 00:24
Álgebra Linear
-
- Quais as diferenças destes termos - algebra
por Soprano » Seg Fev 15, 2016 14:11
- 0 Respostas
- 2109 Exibições
- Última mensagem por Soprano

Seg Fev 15, 2016 14:11
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



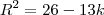 onde a porção da direita tem q ser maior q zero. Isso se da para valores de K maiores que 2 e para uma solução mais formal:
onde a porção da direita tem q ser maior q zero. Isso se da para valores de K maiores que 2 e para uma solução mais formal:![k=]2,\infty[ k=]2,\infty[](/latexrender/pictures/77f37cec0c32678a1b303efc44947fbd.png)




 , avisa que eu resolvo.
, avisa que eu resolvo.

