Enfim, meu professor de calculo passou um trabalho que eu to penando pra fazer, e tou vindo aqui como ultimo recurso antes deu desistir de novo dessa cadeira...
O limite eh o seguinte
![\lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[2]{x-1}-1}](/latexrender/pictures/1a995369b61d86c46d174fe2c5af639c.png "\lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[2]{x-1}-1}")
tentei multiplicar pelos conjugados, mas da sempre indeterminação, depois tenti multiplicar usando a formula dos cubos, mas mesmo assim anda da indeterminação no numerador... eu não sei mais o que fazer.... a ficha da como resultado: 5/6Desculpem raiva, mas esse limite realmente me conseguiu tirar do sério...
![y=\sqrt[n]{u^m}
y=u^\frac{m}{n}](/latexrender/pictures/11377ae512e6f68164781bacc89e9c35.png "y=\sqrt[n]{u^m}
y=u^\frac{m}{n}")
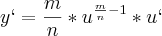
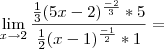
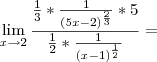
![\lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[]{x-1}-1}](/latexrender/pictures/f2524f9b7bbb771867abdf78bf4cf015.png "\lim_{x\rightarrow2}\frac{\sqrt[3]{5x-2}-2}{\sqrt[]{x-1}-1}")
![\lim_{x\rightarrow2}\frac{\frac{5}{3\sqrt[3]{(5x-2)^2}}}{\frac{1}{2 \sqrt[]{x-1}}}=](/latexrender/pictures/faad4b3512293be3f18e1bb0d1235e11.png "\lim_{x\rightarrow2}\frac{\frac{5}{3\sqrt[3]{(5x-2)^2}}}{\frac{1}{2 \sqrt[]{x-1}}}=")
![\frac{\frac{5}{3\sqrt[3]{(5*2-2)^2}}}{\frac{1}{2\sqrt[]{2-1}}}=](/latexrender/pictures/3f33784e834f30245fa8c4f116e8e632.png "\frac{\frac{5}{3\sqrt[3]{(5*2-2)^2}}}{\frac{1}{2\sqrt[]{2-1}}}=")
![\frac{\frac{5}{3\sqrt[3]{8^2}}}{\frac{1}{2\sqrt[]{1}}}=](/latexrender/pictures/a4932fa4adc9063a7716a1d6bd8782b5.png "\frac{\frac{5}{3\sqrt[3]{8^2}}}{\frac{1}{2\sqrt[]{1}}}=")
![\frac{\frac{5}{3\sqrt[3]{64}}}{\frac{1}{2}}=](/latexrender/pictures/2d7d0c054983784cc915c4aa02a4a60b.png "\frac{\frac{5}{3\sqrt[3]{64}}}{\frac{1}{2}}=")
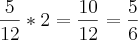
![\lim_{x\rightarrow2}=\frac{\sqrt[3]{5x-2}+\sqrt[3]{8}}{\sqrt[2]{x-1}-1}](/latexrender/pictures/9679ead680d424f566ae214dc39366d0.png "\lim_{x\rightarrow2}=\frac{\sqrt[3]{5x-2}+\sqrt[3]{8}}{\sqrt[2]{x-1}-1}")
.Sendo ![a=\sqrt[3]{5x-2}](/latexrender/pictures/ee60c604b6a2c52d9cdfc17dd6adb3bd.png "a=\sqrt[3]{5x-2}")
e ![b=\sqrt[3]{8}](/latexrender/pictures/4d4896e7b9ae7153f04f389900a1f4f0.png "b=\sqrt[3]{8}")
temos:![\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}=\left(\sqrt[3]{5x-2}-\sqrt[3]{8} \right)](/latexrender/pictures/9d88f13e227b0f373206658d547cc57e.png "\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}=\left(\sqrt[3]{5x-2}-\sqrt[3]{8} \right)")
.Agora jogando no limite,conseguimos:![\lim_{x\rightarrow2}=\frac{\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}}{\sqrt[2]{x-1}-1}](/latexrender/pictures/a65827f640f8c3b7e0c02ce5d81fe499.png "\lim_{x\rightarrow2}=\frac{\frac{{\sqrt[3]{5x-2}}^{3}-{\sqrt[3]{8}}^{3}}{\left({(\sqrt[3]{5x-2})}^{2}+\sqrt[3]{5x-2}\sqrt[3]{8}+{(\sqrt[3]{8})}^{2} \right)}}{\sqrt[2]{x-1}-1}")
.Arrumando um pouco:![\lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}](/latexrender/pictures/6df9f45aa71af00fc73111d0e7d8c350.png "\lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}")
.Agora multiplicando pelo "conjugado" em baixo e em cima:![\lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}.\frac{\sqrt[2]{x-1}+1}{\sqrt[2]{x-1}+1}](/latexrender/pictures/fdbbd98ec8ba95473be3420d90d9ffc4.png "\lim_{x\rightarrow2}=\frac{5(x-2)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(\sqrt[2]{x-1}-1)}.\frac{\sqrt[2]{x-1}+1}{\sqrt[2]{x-1}+1}")
![\Rightarrow \lim_{x\rightarrow2}=\frac{5(x-2)(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(x-2)}](/latexrender/pictures/3d8672ebd6628b4ad5edc58e4d9d4145.png "\Rightarrow \lim_{x\rightarrow2}=\frac{5(x-2)(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).(x-2)}")
.Cortando o (x-2),temos uma função em baixo que só possui raiz complexa e em cima uma que não vai dar zero quando for colocada igual a 2.![\lim_{x\rightarrow2}=\frac{5(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).}=\frac{5(2)}{(4+4+4)}=\frac{5}{6}](/latexrender/pictures/e5a26c3cdebafdb2189873cf10e2370f.png "\lim_{x\rightarrow2}=\frac{5(\sqrt[2]{x-1}+1)}{\left({(\sqrt[3]{5x-2})}^{2}+2\sqrt[3]{5x-2}+4 \right).}=\frac{5(2)}{(4+4+4)}=\frac{5}{6}")
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)