Sejam a, b e c reais não-nulos e distintos , c > 0. sendo a função dada por f(X) = ax + b/ x+ c, então f(X) para c < X < c, é constante e igual a:
a) a + b
b) a + c
c) c
d) b
e) a


para c < X < c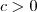 .
.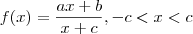 , é constante e igual a:
, é constante e igual a: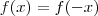 , para todo x do Dom f.
, para todo x do Dom f.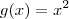
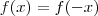 .
.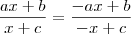

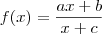
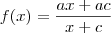
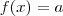 (alternativa e)
(alternativa e)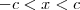 no enunciado, é para garantir a condição de existência da função.
no enunciado, é para garantir a condição de existência da função.
Visitante escreveu:Sejam a, b e c reais não-nulos e distintos , c > 0. sendo a função dada por f(X) = ax + b/ x+ c, então f(X) para c < X < c, é constante e igual a
a) a + b
b) a + c
c) c
d) b
e) a

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



