A)4/3
B)1/2
C)2/3
D)3/4
E)4/9
Eu novamente comecei e o resultado deu em raiz.
Fiz assim:
Volume da esfera:
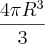
Volume do cone:
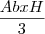
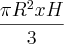
Como ele disse que o cone é equilátero, a altura do cone vai ser a altura do triangulo equilátero
![\frac{\pi{R}^{2}x\left(\frac{{L}\sqrt[]{3}}{2} \right)}{3}](/latexrender/pictures/ed2e2cf65ba105a3c100e032df93ce2e.png "\frac{\pi{R}^{2}x\left(\frac{{L}\sqrt[]{3}}{2} \right)}{3}")
Como o cone é equilatero o lado do cone(geratriz vai ser igual 2R)
![\frac{\pi{R}^{2}x\left(\frac{{2R}\sqrt[]{3}}{2} \right)}{3}](/latexrender/pictures/e397b604ea7def9487a9f640731bb29f.png "\frac{\pi{R}^{2}x\left(\frac{{2R}\sqrt[]{3}}{2} \right)}{3}")
Resolvendo vai dar:
![\frac{{R}^{3}\sqrt[]{3}\pi}{3}](/latexrender/pictures/8bd38ea6943c57b7d0a0bb97b2a2603a.png "\frac{{R}^{3}\sqrt[]{3}\pi}{3}")
Aí a razao:
![\frac{\frac{4\pi{R}^{3}}{3}}{\frac{{R}^{3}\sqrt[]{3}\pi}{3}}](/latexrender/pictures/e50c2858153450af96db39c159d354e9.png "\frac{\frac{4\pi{R}^{3}}{3}}{\frac{{R}^{3}\sqrt[]{3}\pi}{3}}")
Resultado:
![\frac{4\sqrt[]{3}}{3}](/latexrender/pictures/4226b0b2cb49ddc63f2da4c50b05bf0e.png "\frac{4\sqrt[]{3}}{3}")
Gostaria de saber onde estou errando.
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)