 por renataf » Ter Nov 30, 2010 12:47
por renataf » Ter Nov 30, 2010 12:47
Uma esfera de raio R está inscrita num cone equilátero. A razão entre o volume da esfera e o do cone é:
A)4/3
B)1/2
C)2/3
D)3/4
E)4/9
Eu novamente comecei e o resultado deu em raiz.
Fiz assim:
Volume da esfera:
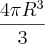
Volume do cone:
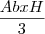
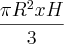
Como ele disse que o cone é equilátero, a altura do cone vai ser a altura do triangulo equilátero
![\frac{\pi{R}^{2}x\left(\frac{{L}\sqrt[]{3}}{2} \right)}{3} \frac{\pi{R}^{2}x\left(\frac{{L}\sqrt[]{3}}{2} \right)}{3}](/latexrender/pictures/ed2e2cf65ba105a3c100e032df93ce2e.png)
Como o cone é equilatero o lado do cone(geratriz vai ser igual 2R)
![\frac{\pi{R}^{2}x\left(\frac{{2R}\sqrt[]{3}}{2} \right)}{3} \frac{\pi{R}^{2}x\left(\frac{{2R}\sqrt[]{3}}{2} \right)}{3}](/latexrender/pictures/e397b604ea7def9487a9f640731bb29f.png)
Resolvendo vai dar:
![\frac{{R}^{3}\sqrt[]{3}\pi}{3} \frac{{R}^{3}\sqrt[]{3}\pi}{3}](/latexrender/pictures/8bd38ea6943c57b7d0a0bb97b2a2603a.png)
Aí a razao:
![\frac{\frac{4\pi{R}^{3}}{3}}{\frac{{R}^{3}\sqrt[]{3}\pi}{3}} \frac{\frac{4\pi{R}^{3}}{3}}{\frac{{R}^{3}\sqrt[]{3}\pi}{3}}](/latexrender/pictures/e50c2858153450af96db39c159d354e9.png)
Resultado:
![\frac{4\sqrt[]{3}}{3} \frac{4\sqrt[]{3}}{3}](/latexrender/pictures/4226b0b2cb49ddc63f2da4c50b05bf0e.png)
Gostaria de saber onde estou errando.
-
renataf
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Sáb Nov 20, 2010 17:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Ter Nov 30, 2010 13:47
por Elcioschin » Ter Nov 30, 2010 13:47
O raio R do cone é diferente do raio r da esfera ----> R > r
Volume da esfera ----> Ve = (4/3)*pi*r³
Cone equilátero ----> gerariz = diâmetro da base = D ----> D = 2*r*V3 ----> Raio da base ----> R = r*V3
Altura do cone equilátero ----> H = 3*r
Volume do cone -----> Vc = (1/3)*pi*(r*V3)²*(3*r) ----> Vc = 3*pi*R³
Ve/Vc = (4/3)/3 ----> Ve/Vc = 4/9
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por renataf » Ter Nov 30, 2010 14:00
por renataf » Ter Nov 30, 2010 14:00
Obrigada pela ajuda, mas eu consegui chegar no resultado, eu tinha esquecido de considerar q o raio da esfera correspondia a 1/3 da altura do cone. Mas mesmo assim, muito abrigada!
-
renataf
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Sáb Nov 20, 2010 17:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- O volume de uma esfera em relação a outra esfera
por Macedo Junior » Sáb Jul 23, 2016 21:01
- 2 Respostas
- 9570 Exibições
- Última mensagem por Macedo Junior

Sáb Jul 23, 2016 23:28
Geometria Plana
-
- Questão sobre esfera e cone
 por oeslle » Qui Out 16, 2008 22:42
por oeslle » Qui Out 16, 2008 22:42
- 4 Respostas
- 4317 Exibições
- Última mensagem por oeslle

Sex Out 17, 2008 19:53
Geometria Espacial
-
- Força resultante sobre a esfera menor
por Cleyson007 » Dom Mai 12, 2013 16:45
- 2 Respostas
- 2958 Exibições
- Última mensagem por Cleyson007

Dom Mai 12, 2013 21:56
Física
-
- Outra Dúvida
por rodsales » Sáb Jun 06, 2009 21:41
- 1 Respostas
- 1500 Exibições
- Última mensagem por Marcampucio

Sáb Jun 06, 2009 22:38
Trigonometria
-
- Outra dúvida
por rodsales » Qui Jun 18, 2009 22:12
- 1 Respostas
- 1439 Exibições
- Última mensagem por Marcampucio

Sex Jun 19, 2009 00:48
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
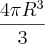
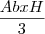
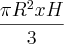
![\frac{\pi{R}^{2}x\left(\frac{{L}\sqrt[]{3}}{2} \right)}{3} \frac{\pi{R}^{2}x\left(\frac{{L}\sqrt[]{3}}{2} \right)}{3}](/latexrender/pictures/ed2e2cf65ba105a3c100e032df93ce2e.png)
![\frac{\pi{R}^{2}x\left(\frac{{2R}\sqrt[]{3}}{2} \right)}{3} \frac{\pi{R}^{2}x\left(\frac{{2R}\sqrt[]{3}}{2} \right)}{3}](/latexrender/pictures/e397b604ea7def9487a9f640731bb29f.png)
![\frac{{R}^{3}\sqrt[]{3}\pi}{3} \frac{{R}^{3}\sqrt[]{3}\pi}{3}](/latexrender/pictures/8bd38ea6943c57b7d0a0bb97b2a2603a.png)
![\frac{\frac{4\pi{R}^{3}}{3}}{\frac{{R}^{3}\sqrt[]{3}\pi}{3}} \frac{\frac{4\pi{R}^{3}}{3}}{\frac{{R}^{3}\sqrt[]{3}\pi}{3}}](/latexrender/pictures/e50c2858153450af96db39c159d354e9.png)
![\frac{4\sqrt[]{3}}{3} \frac{4\sqrt[]{3}}{3}](/latexrender/pictures/4226b0b2cb49ddc63f2da4c50b05bf0e.png)




 .
.



