automóveis constam de sete símbolos sendo três letras,
dentre as 26 do alfabeto, seguidas de quatro algarismos.
a) Quantas placas distintas podemos ter sem o algarismo
zero na primeira posição reservada aos algarismos?
b) No conjunto de todas as placas distintas possíveis,
qual a porcentagem daquelas que têm as duas primeiras
letras iguais?
Na resolução pensei em fazer um grupo de 7 do seguinte jeito:
__ . __ . __ . __ .__ . __. __ =
L L L A A A A
sendo os 3 inicias reservados para letras e os 4 finais aos algarismos,
como é são 26 letras e os algarismos devem ir de 1 a 9,
então ficaria 26x26x26x9x9x9x9=115316136 isso na letra A.
mas a resposta encontrada não está de acordo com a resposta de acordo pelo livro.
Desde já agradeço a ajuda ,



 placas.
placas.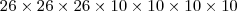 , podemos pensar nas duas primeiras letras como uma só, e realmente são. Portanto estas são
, podemos pensar nas duas primeiras letras como uma só, e realmente são. Portanto estas são  .
.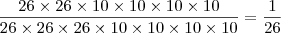 ;
;
