Bom dia.
Não sei nem como começar esta questão...
A primeira probabilidade já me confundiu... Ainda tem a segunda!
Uma urna contém 2 bolas brancas e 3 bolas amarelas distinguíveis apenas pela cor. Aleatoriamente, duas bolas serão escolhidas, sucessivamente e sem reposição, e colocadas em uma segunda urna, na qual há apenas uma bola preta também distinta das demais apenas pela cor. Após a transferência das duas bolas para a segunda urna, escolher-se-á, aleatoriamente, uma única bola dessa urna. Qual a probabilidade de que, nesse último sorteio, a bola escolhida seja amarela?
A resposta correta é: 0,40
Agradeço desde já!!!


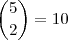 maneiras.
maneiras.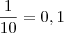
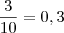

 é resultado da escolha de duas bolas dentre as três amarelas existentes na urna,
é resultado da escolha de duas bolas dentre as três amarelas existentes na urna, 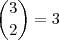 .
. , assim temos uma probabilidade de
, assim temos uma probabilidade de 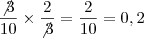 .
. na segunda, ou ainda,
na segunda, ou ainda,  .
.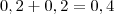 .
.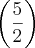 ...
... , mas isto é o mesmo que
, mas isto é o mesmo que  ou
ou  .
. , diferente do caso das bolas amarelas (
, diferente do caso das bolas amarelas ( ,
,  e
e 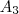 ), onde eu posso formar três pares:
), onde eu posso formar três pares:  .
.
 .
.



