
Determine o valor da área da região interna às duas elipses. (que parece um quadrado deformado)
Eu sei que a área de uma elipse é igual a
 , mas não estou conseguindo desenvolver um método para calcular tal área..
, mas não estou conseguindo desenvolver um método para calcular tal área..alguém tem alguma ideia?


 , mas não estou conseguindo desenvolver um método para calcular tal área..
, mas não estou conseguindo desenvolver um método para calcular tal área..
alexandre32100 escreveu:Victor, usa o sistema de upload de imagem do site, não to conseguindo visualizar a imagem.
Valeu, espero poder te ajudar.



 , facilmente notável igualando as equações das duas.
, facilmente notável igualando as equações das duas.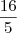 .
.  pra poder prosseguir..
pra poder prosseguir..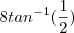




Fantini escreveu:Acredito que o método seja por integral dupla, que no caso teria que dividir em mais de uma região. Ficaria meio chato mas "resolvível".
 ?
?


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



