 por natanskt » Ter Nov 16, 2010 13:02
por natanskt » Ter Nov 16, 2010 13:02
O PAR (X,Y) SOLUÇÃO DA EQUAÇÃO MATRICIAL

.
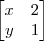
=
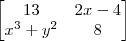
tambem não conseguir fazer essa,ela parece facil
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Pedro123 » Ter Nov 16, 2010 16:44
por Pedro123 » Ter Nov 16, 2010 16:44
Fala natan, blz cara? então, a questão acaba por se resolver com um sistema. Veja bem:
Fazendo a multiplicação de matrizes, no caso, da 1 linha com a 1 coluna, temos:
x² - 4y = 13; agora, fazendo da 2 linha com a segunda coluna:
2x² + y = 8, multiplicando a segunda por 4:
x² - 4y = 13
8x² +4y = 32, agora somando:
9x² = 45
x² = 5 --> x =V5. --> substituindo na 1 equação:
5 - 4y = 13
-4y = 8 --> y = -2.
logo, o par (x,y) = (V5, -2)
confere ai pra ver se é esse o resultado certinho, creio que sim. abraços
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por natanskt » Ter Nov 16, 2010 17:06
por natanskt » Ter Nov 16, 2010 17:06
hey me ajuda nessa duvida daqui
não intendi essa parte eu fiz igual aí
só que...
x²-4y=13 a outra é 2x²+y=8
como faz pra sair daqui,não intendi,me ajuda ae bem explicadinho
vlw
tem que dar raiz de 5 e -2 sua resposta ta certa
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Pedro123 » Ter Nov 16, 2010 17:13
por Pedro123 » Ter Nov 16, 2010 17:13
bem que que aconteceu, eu cheguei nessa parte certo?
x² - 4y = 13;
2x² + y = 8
veja que isto é um sistema (2 variaveis e 2 equações), que tem varios jeitos de se resolver, eu escolhi o metodo da adição, so que pra fazer isso, tiver de multiplicar uma das duas pra poder tirar uma das variaveis, mas se vc nao entendeu faça o seguinte, isole o Y, e depois substitua na outra que da na mesma, tipo assim:
x²- 4y = 13 --> -4y = 13 - x² --> y = (13 - x²)/ -4 --> y = (x² - 13) / 4
ai vc pega esse y, e substitui no y da outra equação que vc vai conseguir resolver entendeu?
qualquer duvida, é so mandar abraçoss
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por Pedro123 » Sex Nov 19, 2010 12:11
por Pedro123 » Sex Nov 19, 2010 12:11
hahah beleza mano, relaxa que isso, tente o seguinte então:
x² - 4y = 13;
2x² + y = 8
a gente tinha isolado o Y de cima correto? tente agora fazer o contrário, isolar o Y de baixo e depois substituir em cima EX:
2x² + y = 8 --> y = 8 - 2x² ai depois joga no outro, consegui partir daqui?? abrasss qualquer coisa fala ae
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (EEAR)-MATRIZ
por natanskt » Qua Nov 17, 2010 09:49
- 3 Respostas
- 3499 Exibições
- Última mensagem por natanskt

Qua Nov 17, 2010 15:48
Matrizes e Determinantes
-
- (EEAR)-SISTEMAS LINEARES(MATRIZ)
por natanskt » Qui Nov 25, 2010 13:16
- 1 Respostas
- 3106 Exibições
- Última mensagem por Elcioschin

Qui Nov 25, 2010 16:01
Matrizes e Determinantes
-
- (EEAR)Função
 por natanskt » Sex Out 15, 2010 19:08
por natanskt » Sex Out 15, 2010 19:08
- 6 Respostas
- 6609 Exibições
- Última mensagem por DanielRJ

Sáb Out 16, 2010 16:57
Funções
-
- (EEAR)Função
por natanskt » Sex Out 15, 2010 19:18
- 4 Respostas
- 6090 Exibições
- Última mensagem por Elcioschin

Sáb Out 16, 2010 19:13
Funções
-
- (EEAR)Função
por natanskt » Ter Out 19, 2010 10:40
- 1 Respostas
- 2468 Exibições
- Última mensagem por DanielRJ

Ter Out 19, 2010 16:37
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.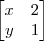 =
=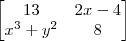

 .
.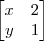 =
=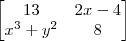




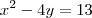
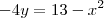


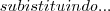



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
