Gostaria de saber se a resolução do exercício abaixo está correta. Desde já agradeço pela boa vontade, que Deus o abençoe.
A questão é o seguinte: ------->>>> A sequência
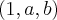 é uma progressão aritmética e a sequência
é uma progressão aritmética e a sequência  é uma progressão geométrica não constante. O valor de a é:
é uma progressão geométrica não constante. O valor de a é:a)
 b)
b)  c)
c)  d)
d) 

e)

Eu resolvi da seguinte maneira-----> Para encontrar a razão da PA

Para encontrar a razão da PG
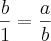
Montei o seguinte sistema, para encontrar os valores correspondentes a a e b ----->


A partir do sistema encontrei os valores de b=1 e a=1
Marcando a alternativa c como correta.
Um forte abraço.
Até mais.



 :
:
 não convém como solução desta equação do segundo grau, pois neste caso a progressão geométrica teria razão 1 e seria constante.
não convém como solução desta equação do segundo grau, pois neste caso a progressão geométrica teria razão 1 e seria constante. , considere a outra raiz
, considere a outra raiz 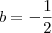 .
.



 .
.



