 por macburn » Sáb Nov 06, 2010 12:16
por macburn » Sáb Nov 06, 2010 12:16
Olá pessoal,
Bom dia, como vai vocês??? Bom vi essa expressão em uma bibliografia e ele afirma que para chegar a expressão final apenas multiplica-se por

ambos os membros da equação. Não consegui, alguém poderia me dar uma luz por gentileza.
![I{}_{\eta}=\sqrt[2]{\frac{p{}_{f}}{R{}_{`}}} I{}_{\eta}=\sqrt[2]{\frac{p{}_{f}}{R{}_{`}}}](/latexrender/pictures/a673147d6ce293b12dc2419d9587e362.png)
essa é a equação que deve ser multiplicada ambos os lados por

.
Lembrando que:
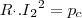
A expressão final fica:
![I{}_{\eta} = \sqrt[2]{\frac{p{}_{f}}{p{}_{c}}} I{}_{\eta} = \sqrt[2]{\frac{p{}_{f}}{p{}_{c}}}](/latexrender/pictures/b79ef6b494ab3b5d9b25355ddcc4fb9e.png)
Abraços pessoal...
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por andrefahl » Sáb Nov 06, 2010 13:21
por andrefahl » Sáb Nov 06, 2010 13:21
Olá Macburn,
bom duas coisas, ja tentou isolar o R e subtituir na eq?
mas mm assim eu tentei e ainda sim sobra um
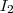
no outro lado multiplicando a raiz...
a eq resultante esta correta?
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por macburn » Sáb Nov 06, 2010 13:47
por macburn » Sáb Nov 06, 2010 13:47
Boa tarde pessoal,
Oh Andre, acho que cometi um equívoco. Ao invés de multiplicar como disse é dividir ambos os termos por

. Me equivoquei. Mas será que agora dá certo??
Abraços amigão
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por macburn » Sáb Nov 06, 2010 14:03
por macburn » Sáb Nov 06, 2010 14:03
Pessoal,
Dividindo e fazendo como o andre disse isolando o
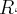
dá certo.
meus agradecimentoos pessoal
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calcular XV dessa equação] ( Confuso !! )
por Andre Lopes » Sex Ago 30, 2013 13:08
- 0 Respostas
- 1062 Exibições
- Última mensagem por Andre Lopes

Sex Ago 30, 2013 13:08
Funções
-
- Interpretação dessa questão
por Joelson » Dom Jun 21, 2009 17:22
- 2 Respostas
- 2930 Exibições
- Última mensagem por Joelson

Dom Jun 21, 2009 19:13
Álgebra Elementar
-
- Determinante dessa matriz?
por Carolziiinhaaah » Qui Jun 24, 2010 11:45
- 2 Respostas
- 2470 Exibições
- Última mensagem por Carolziiinhaaah

Qui Jun 24, 2010 12:33
Matrizes e Determinantes
-
- Galera preciso dessa resolução
por Justiceira » Dom Set 27, 2009 13:33
- 3 Respostas
- 2256 Exibições
- Última mensagem por Cleyson007

Dom Set 27, 2009 16:54
Trigonometria
-
- Quero saber dessa integral
por baianinha » Qui Dez 16, 2010 12:35
- 1 Respostas
- 1675 Exibições
- Última mensagem por Moura

Qui Dez 16, 2010 14:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ambos os membros da equação. Não consegui, alguém poderia me dar uma luz por gentileza.
ambos os membros da equação. Não consegui, alguém poderia me dar uma luz por gentileza.![I{}_{\eta}=\sqrt[2]{\frac{p{}_{f}}{R{}_{`}}} I{}_{\eta}=\sqrt[2]{\frac{p{}_{f}}{R{}_{`}}}](/latexrender/pictures/a673147d6ce293b12dc2419d9587e362.png) essa é a equação que deve ser multiplicada ambos os lados por
essa é a equação que deve ser multiplicada ambos os lados por  .
.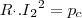
![I{}_{\eta} = \sqrt[2]{\frac{p{}_{f}}{p{}_{c}}} I{}_{\eta} = \sqrt[2]{\frac{p{}_{f}}{p{}_{c}}}](/latexrender/pictures/b79ef6b494ab3b5d9b25355ddcc4fb9e.png)


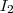 no outro lado multiplicando a raiz...
no outro lado multiplicando a raiz...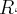 dá certo.
dá certo.