 por macburn » Ter Nov 02, 2010 15:51
por macburn » Ter Nov 02, 2010 15:51
Olá pessoal,
Como vai? Estou estudando um assunto da minha área de Engenharia Elétrica e trombei com essa integral. Me formei há muito tempo, então gostaria de uma força de vocês para solucioná-la. Bom, o D(t) chama-se demanda de pico em kW no intervalo de tempo considerado, T (horas ou minutos).
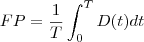
Um abraço pessoal!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Neperiano » Ter Nov 02, 2010 18:14
por Neperiano » Ter Nov 02, 2010 18:14
Ola
Pode ser que eu esteja enganado, mas é só integral o d, como se fosse x, que fica (x^2)/2 e aplica o T no lugar do x - aplicando o 0 e multiplicar as duas por 1/T
Eu acho que é isso, se não for pergunte denovo que talvez não tenha entendido
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por macburn » Ter Nov 02, 2010 19:10
por macburn » Ter Nov 02, 2010 19:10
Boa noite pessoal,
Como vao? Será que algum dos colegas poderia resolvê-la numericamente por gentileza, sem querer abusar da boa vontade dos nobres amigos?
Um abraço pessoal
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Neperiano » Ter Nov 02, 2010 20:22
por Neperiano » Ter Nov 02, 2010 20:22
Ola
Como quiser, posso sim, só peço desculpa por não saber usar latex
A integral de D(t) é [D^2(t)]/2 a partir dai aplique os limites da integral
[D^2(T)]/2 - [D^2(0)]/2
Como a segunda vai dar zero, só precisa aplicar o 1/T na primeira
1/T . [D^2(T)/2, voce pode cortar os T e fica = (D^2)/2
Cara eu acho que é isso, mas como falei posso estar enganado.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por macburn » Ter Nov 02, 2010 21:33
por macburn » Ter Nov 02, 2010 21:33
Boa noite meu nobre,
Como vai? Meus sinceros agradecimentos rapaz. Sua ajuda foi de grande valia. Parabéns pela boa vontade em ajudar.
Um grande abraço,
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por andrefahl » Qua Nov 03, 2010 03:29
por andrefahl » Qua Nov 03, 2010 03:29
Olá meus caros,
estava olhando esse tópico e acho que o Maligno deve ter confundido
D(t) é a demanda de pico em função do tempo
seria a mesma coisa que falarmos em uma função qualquer f(x)
então não se pode resolver a função D(t) como se fosse um polinômio, como foi feito no exemplo
pois não conhecemos a tal função (D(t)).
Por exemplo se tivermos

entaum temos

daí resulta
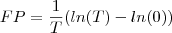
e não no resultado anterior.
Portanto a integral é a definição da função, se D(t) é polinomio, exponencial, logaritmica, etc...
cada uma tem um jeito diferente de resolver =) vai depender de qual for a função D(t)
entaum para resolver a equação deve-se conhecer a função D(t)
Espero ter ajudado...
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por Neperiano » Qua Nov 03, 2010 12:35
por Neperiano » Qua Nov 03, 2010 12:35
Ola
Poise eu até disse que poderia estar errado porque nunca integrei uma função dentro de outra, tentei usar o u ali, como se fosse ln u, no caso D(u), mas não sei se pode.
Macburn se voce tiver a resposta ai pra ve se realmente o andrefahl esta certo
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por andrefahl » Qua Nov 03, 2010 14:37
por andrefahl » Qua Nov 03, 2010 14:37
HASUDhAUSHDUASHDUASHd
acho que vc não entendeu Maligno =)
imagine só vc tem o seguinte:
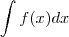
como vc resolve isso?
se você não sabe qual a

o maximo que você pode afirmar é que
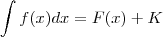
onde F(x) é uma primitiva da função f(x) tq F´(x) = f(x)
correto?
se f(x) = x, dai sim vc pode resolver da forma que vc citou no começo que a integral d x é

e se f(x) fosse

?? e se fosse uma outra função maluca qualquer? por enquanto sem saber qual a função
vc não pode nem usar a mudança de variavel =).
que eu coloquei com o resultado dando ln(T) e talz... foi apenas uma suposição, se

...
mas se for outra dará outro resultado o qual não conhecemos pois não sabemos qual é D(t).
ficou um pouco mais claro?
se o Macburn colocar uma função de demanda de pico em kW podemos ajudar melhor na resolução.
Att
André
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por macburn » Qua Nov 03, 2010 16:22
por macburn » Qua Nov 03, 2010 16:22
Olá pessoal,
Muito boa tarde, como vai vocês? Bom na minha opinião, de acordo com a bibliografia, D(t) é a demanda de pico em kW no intervalo de tempo considerado, onde T pode ser em horas ou minutos. Creio que esse D é um valor medido em um determinado período. Então por exemplo, se num período de 1hora foi medido 75kW, 75kW é o valor do D e (t) penso que deva ser 1hora. Se for isso pessoal, como seria a solução. A princípio creio que não exista uma função implícita como o andrefahl nos alertou.
Meus agradecimentos meu nobre!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por andrefahl » Qua Nov 03, 2010 16:57
por andrefahl » Qua Nov 03, 2010 16:57
Bom se acaso D(t) for constante e igual a 75kW temos o seguinte:

dai é só substituir o valor para o tempo que vc deseja encontrar.
Muito importante! isso só valerá caso D(t) seja constante.
Estou batendo muito nessa tecla, pois se D(t) não for constante no intervalo de tempo desejado
a integral fica diferente =)
mas se for constante é resolvida dessa maneira.
Cara, qual o livro que tem isso, pq após eu resolver algo ficou estranho, T/T = 1... qnt ao processo de integração eu tenho crtz q está correto
só tenho duvida na definição da função ...
Att.
André
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por MarceloFantini » Qua Nov 03, 2010 17:06
por MarceloFantini » Qua Nov 03, 2010 17:06
Isso também está com cara do teorema do valor médio para integrais:
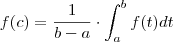
O que chega a ser coerente com a interpretação de demanda de pico (acho).
P.S.: Boa sorte como diretor de patrimônio, André! Haha.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por macburn » Qua Nov 03, 2010 17:35
por macburn » Qua Nov 03, 2010 17:35
Olá pessoal,
BOm, onde tem essa fórmula é num livro de engenharia elétrica. Penso que como o nosso amigo Fantini salientou, pode ser essa questão do valor médio. Bom, quando chegar em casa, vou tentar localizar essa fórmula no livro pois é uma referência de uma dissertação de mestrado de um colega que estou dando uma lida. Pessoal, uma dúvida. Teria como eu resolver essa integral de outra maneira por exemplo, transformar em somatórios e tal.
Abraços meus nobres
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Qua Nov 03, 2010 18:20
por MarceloFantini » Qua Nov 03, 2010 18:20
Tudo depende da função
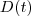
como o colega André disse. Não temos como afirmar mais nada sem saber a função. Talvez o que o livro queira dizer é que o modo de calcular a demanda de pico é o valor médio da integral do tempo inicial zero até o instante que se quer, sendo que a função pode variar dependendo do aparelho ou algo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por macburn » Qua Nov 03, 2010 19:42
por macburn » Qua Nov 03, 2010 19:42
Boa noite pessoal,
Bom Fantini, penso que é isso mesmo que você postou! "Talvez o que o livro queira dizer é que o modo de calcular a demanda de pico é o valor médio da integral do tempo inicial zero até o instante que se quer, sendo que a função pode variar dependendo do aparelho ou algo." Sendo assim, penso que a forma de calcular é aquela mesma que você mencionou!
Abraços amigão!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por macburn » Qui Nov 04, 2010 11:30
por macburn » Qui Nov 04, 2010 11:30
OLá pessoal,
Como vão vocês. COnversando com o professor, uma maneira de resolvermos essa integral pelo Excel seria dessa forma:
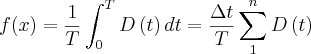
onde

é o intervalo de tempo considerado ou seja, de tantos em tantos minutos ou horas, e o T seria o período por exemplo se 24 horas T =24, se 2 dias T = 48.
Pessoal, minha dúvida é como ele chegou a essa equação!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Qui Nov 04, 2010 11:39
por MarceloFantini » Qui Nov 04, 2010 11:39
Isso lembra a definição de integral, sem o limite.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por macburn » Qui Nov 04, 2010 14:43
por macburn » Qui Nov 04, 2010 14:43
Boa tarde,
Olá grande Fantini, tudo bom? então você já resolver através do excel alguma derivada ou integral? Mas minha dúvida é se está certo essa igualdade!!!
Abraços!
-
macburn
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Ter Nov 02, 2010 14:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Qui Nov 04, 2010 17:20
por MarceloFantini » Qui Nov 04, 2010 17:20
Nunca resolvi pelo Excel, mas tenho minhas dúvidas se está certo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ângulo numa elipse
por Jhenrique » Seg Out 08, 2012 21:20
- 1 Respostas
- 1004 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 21:46
Geometria Analítica
-
- [PA] Uma dúvida numa questão de PA
por rochadapesada » Qui Abr 04, 2013 22:08
- 3 Respostas
- 2637 Exibições
- Última mensagem por DanielFerreira

Dom Abr 07, 2013 20:28
Progressões
-
- Dúvida numa exercíco
por carlota_almada » Dom Dez 04, 2016 13:17
- 1 Respostas
- 2353 Exibições
- Última mensagem por Cleyson007

Seg Dez 05, 2016 20:35
Polinômios
-
- Coordenadas de 8 pontos numa circunferencia
 por cristfc » Qua Nov 05, 2008 15:43
por cristfc » Qua Nov 05, 2008 15:43
- 3 Respostas
- 3078 Exibições
- Última mensagem por edwinaclima

Sáb Jul 10, 2010 11:44
Trigonometria
-
- Duvida numa funçao definida por ramos
por AnaOliveira » Sáb Abr 30, 2011 16:54
- 12 Respostas
- 7420 Exibições
- Última mensagem por NMiguel

Dom Mai 01, 2011 19:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
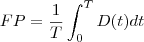





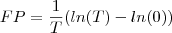
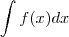 como vc resolve isso?
como vc resolve isso? o maximo que você pode afirmar é que
o maximo que você pode afirmar é que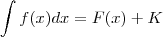 onde F(x) é uma primitiva da função f(x) tq F´(x) = f(x)
onde F(x) é uma primitiva da função f(x) tq F´(x) = f(x)
 ?? e se fosse uma outra função maluca qualquer? por enquanto sem saber qual a função
?? e se fosse uma outra função maluca qualquer? por enquanto sem saber qual a função ...
...
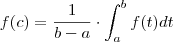


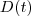 como o colega André disse. Não temos como afirmar mais nada sem saber a função. Talvez o que o livro queira dizer é que o modo de calcular a demanda de pico é o valor médio da integral do tempo inicial zero até o instante que se quer, sendo que a função pode variar dependendo do aparelho ou algo.
como o colega André disse. Não temos como afirmar mais nada sem saber a função. Talvez o que o livro queira dizer é que o modo de calcular a demanda de pico é o valor médio da integral do tempo inicial zero até o instante que se quer, sendo que a função pode variar dependendo do aparelho ou algo.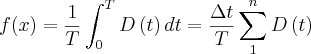
 é o intervalo de tempo considerado ou seja, de tantos em tantos minutos ou horas, e o T seria o período por exemplo se 24 horas T =24, se 2 dias T = 48.
é o intervalo de tempo considerado ou seja, de tantos em tantos minutos ou horas, e o T seria o período por exemplo se 24 horas T =24, se 2 dias T = 48.