![{log}_{\frac{1}{2}} \frac{\sqrt[]{2}}{2} = \frac{1}{2}](/latexrender/pictures/551333c32a1d349b21a7dba84f96662c.png "{log}_{\frac{1}{2}} \frac{\sqrt[]{2}}{2} = \frac{1}{2}")
Boa tarde, no livro que utilizo há duas questão com esse cálculo e não consigo entender.
>> Qual é a base de um sistema logaritmico, onde o lagaritmo é
e o antilogaritmo é ![\frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png "\frac{\sqrt[]{2}}{2}")
?Sei que a base sera meio porque nos próximos exercícios aparece o seguinte:
>> Calcule o valor de "x", e modo que se tenha
Ambos exercícios eu sei o gabarito, mas não sei como chegar na resposta fazendo o exercício.
De qualquer modo, grata.
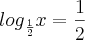voce tem elevar a 
a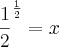
![\sqrt[2]{\frac{1}{2}}=x](/latexrender/pictures/09d9edb0078ca741a0b74a6d8592af4f.png "\sqrt[2]{\frac{1}{2}}=x")
![\frac{1}{\sqrt[2]{2}}=x](/latexrender/pictures/befd28698d2ec6910e488563017891fc.png "\frac{1}{\sqrt[2]{2}}=x")
![\frac{1.\sqrt[2]{2}}{{\sqrt[2]{2}}_{\sqrt[2]{2}}}](/latexrender/pictures/599cca0c8a8c41338bf5afc05c4fce97.png "\frac{1.\sqrt[2]{2}}{{\sqrt[2]{2}}_{\sqrt[2]{2}}}")
![\frac{\sqrt[2]{2}}{\sqrt[2]{4}}=x](/latexrender/pictures/9ba06359908689394634dd77a2d206c4.png "\frac{\sqrt[2]{2}}{\sqrt[2]{4}}=x")
![\frac{\sqrt[2]{2}}{2}=x](/latexrender/pictures/ab64d95a887d88d0ac35189c957fd632.png "\frac{\sqrt[2]{2}}{2}=x")
![\frac{1}{\sqrt[2]{2}} = x](/latexrender/pictures/7d44153851b838dc4a225d2a5fe1e32f.png "\frac{1}{\sqrt[2]{2}} = x")
)
o numerador da fração se torna o expoente do numero 2 e o denominador se torna o indice da raiz![\sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png "\sqrt[3]{2}")
![{8}^{\frac{2}{3}}= \sqrt[3]{{8}^{2}}= \sqrt[3]{64}](/latexrender/pictures/00eac0ae2a79cedfd9add79bb272a3f3.png "{8}^{\frac{2}{3}}= \sqrt[3]{{8}^{2}}= \sqrt[3]{64}")
por