Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por admin » Sáb Jul 21, 2007 01:22
por admin » Sáb Jul 21, 2007 01:22
Um réu foi condenado por um juri à prisão perpétua. Mas posteriormente, sua pena foi reduzida à metade. Como sua pena pode ser cumprida?
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por jose reis pimenta » Ter Nov 13, 2007 20:00
por jose reis pimenta » Ter Nov 13, 2007 20:00
Como não se pode prever a quantidade de tempo viverá o réu e se não pode prejudicá-lo, o certo e liberá-lo imediatamente.
-
jose reis pimenta
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Nov 11, 2007 19:55
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Nov 13, 2007 21:36
por admin » Ter Nov 13, 2007 21:36
jose reis pimenta escreveu:Como não se pode prever a quantidade de tempo viverá o réu e se não pode prejudicá-lo, o certo e liberá-lo imediatamente.
Considerando a acepção do termo
perpétuo: que dura para sempre, que é eterno.
Uma prisão perpétua, por um tempo perpétuo, quantitativa e matematicamente falando, é um tempo infinito.
As operações com o infinito representam um assunto delicado.
Mas, neste caso, sem perda de generalidade, podemos fazer uma bijeção entre uma medida de tempo escolhida e o conjunto dos números naturais, por exemplo. A quantidade de números é infinita, assim como o tempo perpétuo na medida adotada.
Feita esta consideração, o tempo T de prisão deverá ser:
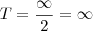
Ou seja, desde que não se envolva outro

nestas divisões do tempo, a prisão continuará sendo perpétua.
Corrijam-me se eu estiver errado.
Abraços!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por wiljrebec » Qua Jan 02, 2008 23:34
por wiljrebec » Qua Jan 02, 2008 23:34
esse problema é tipo uma pegadinha, não dá para calcular o tempo que o réu vai ficar preso . se foi diminuida pela metade é mais conveniente deixá-lo um dia preso e um dia solto até sua morte.
-
wiljrebec
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jan 02, 2008 17:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 2° grau completo
 por Neperiano » Qui Out 30, 2008 16:12
por Neperiano » Qui Out 30, 2008 16:12
Ola
Voce esta certo Fábio pois infinito dividido por 2 continua sendo infinito.
Ah gostei da sua opinião wiljrebec sobre cumprir a pena um dia sim e outro não, mas acho que seria mais fácil, passar 12 horas na cadeia e 12 em casa, ou seja, denoite na prisão e durante o dia em casa.
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por felipe correa » Qui Dez 11, 2008 21:30
por felipe correa » Qui Dez 11, 2008 21:30
eu lembro que eu vi esse problema no livro "o homem que calculava", a solução dele era deixar o prioneiro preso uma determinada quantidade de tempo e depois deixá-lo livre por iqual periodo, depois recomeça o ciclo. assim consequiria-se uma aproximação de metade do perpétuo.
-
felipe correa
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Dez 10, 2008 19:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática computacional
- Andamento: cursando
 por Sandra Piedade » Sáb Dez 13, 2008 13:41
por Sandra Piedade » Sáb Dez 13, 2008 13:41
É interessante este problema! Concordo com o Fábio. Seguindo as outras linhas de raciocínio, o prisioneiro deve estar tanto tempo preso, como em liberdade (pela definição de metade), mas como não sabemos se ele morre no instante já a seguir ou daqui a 80 anos, como decidir quando estará preso? Poderíamos pensar numa correspondência entre tempo e os números reais positivos e pensar numa função que fizesse corresponder 1 aos instantes em que ele estivesse preso e 0 aos restantes, com a condição de que a quantidade de tempo em que estivesse preso teria que ser da mesma cardinalidade do tempo em que estivesse liberto. Pensando nos números racionais e irracionais positivos, e fazendo corresponder, por exemplo os tempos irracionais aos instantes de presídio e os tempos racionais aos de liberdade, de facto são ambos infinitos, mas há muito mais números irracionais do que racionais, a cardinalidade de um é um infinito muito maior que a cardinalidade de outro, por isso mesmo assim não servia para determinar a solução desta questão. Mais uma vez, o Fábio tem razão, metade de infinito é infinito e ainda acrescento que metade de um infinito grande é o mesmo infinito grande (que é a cardinalidade dos números reais). Muito interessante esta questão. Ainda me lembro de, no meu primeiro emprego ter uma discussão com a directora que afirmava que "infinito é um número muito grande"... sem comentários...
Há três tipos de matemáticos: os que sabem contar e os que não sabem contar.
(perdão mas já não me lembro da origem da frase)
-

Sandra Piedade
- Colaborador - em formação

-
- Mensagens: 40
- Registrado em: Ter Set 30, 2008 07:25
- Localização: Setúbal, Portugal
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic em Ensino da Matemática (Portugal)
- Andamento: cursando
-
 por Paulo Beto » Ter Jul 28, 2009 09:58
por Paulo Beto » Ter Jul 28, 2009 09:58
Como a pena foi reduzida à metade, ele fica 12 horas na cadeia e 12 fora dela, todos os dias.
-
Paulo Beto
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jul 27, 2009 23:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por nogueira » Qui Out 01, 2009 17:42
por nogueira » Qui Out 01, 2009 17:42
seguindo que ele tem que ficar um tempo x em casa e outro tempo x na cadeia...... como determinar esse tempo, pois se comecarmos com ele na cadeia e ele morrer antes de cumprir o tempo em casa, nao tera sido a metade, logo devemos reduzir esse tempo, mas ai tem umproblema reduzir até quanto.......em matematica, mesmo se resolvermos deixar ele solto 1 segundo e preso outro segundo, o problema eprsiste.
Mas no campo juridico a solução é facil, como o reu nao deve ser prejudicado, basta alternar um mesmo tempo preso e outro solto, no entanto, iniciamos com ele solto, pois se ele morrer tera ficado mais tempo solto(pró-reu)
-
nogueira
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Out 01, 2009 17:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: lic contabeis
- Andamento: cursando
 por Luiz Augusto Prado » Sex Nov 27, 2009 20:36
por Luiz Augusto Prado » Sex Nov 27, 2009 20:36
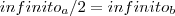
Se deixar um prisioneiro com este tipo de pena sair da cadeia um dia que seja ele não volta mais.
Se ele vivesse perpétuamente (

), este perpétuo é igual ou diferente do perpétuo da pena (

)?
Como ninguem vive para sempre, ele ficará até o ultimo dia de vida na cadeia.
-

Luiz Augusto Prado
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Nov 27, 2009 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




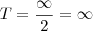
 nestas divisões do tempo, a prisão continuará sendo perpétua.
nestas divisões do tempo, a prisão continuará sendo perpétua.






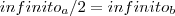
 ), este perpétuo é igual ou diferente do perpétuo da pena (
), este perpétuo é igual ou diferente do perpétuo da pena ( )?
)? 


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.