Preciso de ajuda para resolver e entender essa questão. Desde já agradeço.
Na reforma da cozinha da casa, João utilizou um tipo de cerâmica de 40cm por 40cm, vendido em caixas com 10 unidades a 96 reais cada caixa. O piso da cozinha possui formato retangular cujas medidas são 2,5m por 4,8m e foi todo recoberto com essa cerâmica. A despesa de João com a compra dessa cerâmica para o piso, na reforma da cozinha foi de quanto?


 e a cozinha é dada por
e a cozinha é dada por 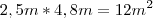 .
. .
. chegamos num total de r$ 720,00.
chegamos num total de r$ 720,00.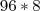 chegamos num total de r$ 768,00. (e sobraria 5 pisos).
chegamos num total de r$ 768,00. (e sobraria 5 pisos).

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)