Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Molina » Dom Abr 25, 2010 14:47
por Molina » Dom Abr 25, 2010 14:47
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Dom Abr 25, 2010 22:04
por Neperiano » Dom Abr 25, 2010 22:04
Ola
Eu naum vou responder, mas creio que para calcular a area do triangulo basta traçar outros triangulos ao lado, aonde há a linha reta para que possa saber o valor do lado, do quadrado é só multiplicar
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Seg Abr 26, 2010 22:21
por Molina » Seg Abr 26, 2010 22:21
Maligno escreveu:Ola
Eu naum vou responder, mas creio que para calcular a area do triangulo basta traçar outros triangulos ao lado, aonde há a linha reta para que possa saber o valor do lado, do quadrado é só multiplicar

Vou dar as alternativas pra ajudar:
a)

b)
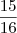
c)

d)

e)

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Douglasm » Ter Abr 27, 2010 13:39
por Douglasm » Ter Abr 27, 2010 13:39
Olá Molina! Bacana este problema. Eu encontrei a alternativa
d) 
usando geometria analítica. Veja só:
Primeiro defini um sistema cartesiano de origem (0,0) no ponto na extremidade inferior esquerda. A partir daí resolvi encontrar a equação de um reta que passar por (0,3) e (3,1) (reta essa, paralela ao lado maior do triângulo). Assim achei:
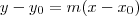
, sendo

(reta decrescente e

é o menor ângulo que a reta forma com a horizontal)
Deste modo:
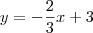
Ok. Agora o que fiz foi encontrar a intersecção dessa reta com as retas

e

(paralelas aos lados direito e superior do quadrado, respectivamente.). Fazendo isso, podemos encontrar as medidas do pequeno triângulo que fica fora do triângulo que contém o quadrado:
1º - Intersecção entre

e

:


O ponto de intersecção tem coordenadas (0,5/3) e o vértice coordenadas (0,2). É fácil notar que o primeiro lado do pequeno triângulo vale 1/3.
2º - Intersecção entre

e

:

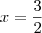
A distância desta intersecção ao vértice vale 1/2.
Agora é só subtraírmos da área do quadrado a área deste pequeno triângulo:

=
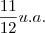
Seria essa a resposta?
Até a próxima.
EDIT: Inverti as coordenadas, agora já está certo.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Ter Abr 27, 2010 15:12
por Molina » Ter Abr 27, 2010 15:12
Boa tarde, Douglas.
A resposta está certa sim. Gostei da forma que você resolveu.
Vou colocar aqui meu modo de solução (e modo da organização das olimpíadas):
É fácil perceber que o lado do triângulo intercepta a parte superior do quadrado no ponto médio deste segmento. Então a base do 'triângulo menor'* nós já temos, que é:
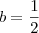
.
* Entende-se pela área do quadrado que é comum a área do triângulo.Precisamos agora achar a altura deste triângulo menor, para calcular sua área e posteriormente retirar da área do quadrado. Para isso usaremos semelhança de triângulos.

- imagem.JPG (5.09 KiB) Exibido 3447 vezes




O que nos garante que a altura do triângulo menor (que estávamos procurando a área) é

Logo a área do triângulo menor é:
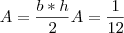
A área total do quadrado é 1, logo a área comum as duas figuras é


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Douglasm » Ter Abr 27, 2010 16:31
por Douglasm » Ter Abr 27, 2010 16:31
Olá Molina. Esse seu método é muito mais objetivo. Eu não tinha me tocado que podia afirmar que o lado de cima do triângulo menor era 1/2, assim seria bem mais rápido.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Ter Abr 27, 2010 18:04
por Molina » Ter Abr 27, 2010 18:04
Douglasm escreveu:Olá Molina. Esse seu método é muito mais objetivo. Eu não tinha me tocado que podia afirmar que o lado de cima do triângulo menor era 1/2, assim seria bem mais rápido.
Até a próxima.
Na verdade eu não afirmei. Pensa o seguinte:
G é ponto médio de PM
Com isso F é ponto médio de PN
H é ponto médio de MN e consequentemente ponto médio de AB.
Por isso AH = HB = DF = FC = 0,5.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Douglasm » Ter Abr 27, 2010 19:30
por Douglasm » Ter Abr 27, 2010 19:30
Exatamente =P. Só depois de ler como você fez é que pude notar isso. Sorte que temos a geometria analítica para nos garantir um resultado, mesmo que normalmente exija mais trabalho braçal! Espero por mais desafios (cheguei a tentar um pouco aquele dos dados, mas parece ser dureza...)
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- OBM-2010
por gabriel_93 » Dom Set 25, 2011 13:53
- 0 Respostas
- 1091 Exibições
- Última mensagem por gabriel_93

Dom Set 25, 2011 13:53
Geometria Plana
-
- Terceira fase OBM 2010
por victoreis1 » Dom Out 24, 2010 16:14
- 4 Respostas
- 3535 Exibições
- Última mensagem por al-mahed

Sáb Dez 11, 2010 21:55
Desafios Difíceis
-
- [polinomios] unifacs 2010.2
por radfmega » Dom Out 06, 2013 11:28
- 2 Respostas
- 1858 Exibições
- Última mensagem por radfmega

Dom Out 06, 2013 15:35
Polinômios
-
- [Funções] Questão Vestibular UFV PASES 2010
por ronaldoudi » Qua Out 12, 2011 23:06
- 0 Respostas
- 1288 Exibições
- Última mensagem por ronaldoudi

Qua Out 12, 2011 23:06
Sistemas de Equações
-
- Revista Veja - Edição 2165 / 19 de maio de 2010
 por Molina » Qua Mai 26, 2010 20:07
por Molina » Qua Mai 26, 2010 20:07
- 1 Respostas
- 3607 Exibições
- Última mensagem por Neperiano

Dom Ago 14, 2011 14:32
Assuntos Gerais ou OFF-TOPIC
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







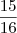




 usando geometria analítica. Veja só:
usando geometria analítica. Veja só: 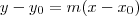 , sendo
, sendo  (reta decrescente e
(reta decrescente e  é o menor ângulo que a reta forma com a horizontal)
é o menor ângulo que a reta forma com a horizontal)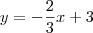
 e
e  (paralelas aos lados direito e superior do quadrado, respectivamente.). Fazendo isso, podemos encontrar as medidas do pequeno triângulo que fica fora do triângulo que contém o quadrado:
(paralelas aos lados direito e superior do quadrado, respectivamente.). Fazendo isso, podemos encontrar as medidas do pequeno triângulo que fica fora do triângulo que contém o quadrado:  e
e  :
:

 e
e  :
:
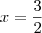
 =
= 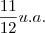

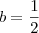 .
.











 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?