Achei esta questão interessante pelo mix de probabilidade e geometria e pensei em compartilhar com vocês.



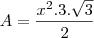

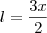
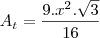

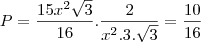
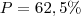

 o lado do Hexágono, a área do Hexágono será a área de seis triângulos equiláteros que o compõe, uma vez que este é regular. Logo, teremos que há seis triângulos de lados medindo
o lado do Hexágono, a área do Hexágono será a área de seis triângulos equiláteros que o compõe, uma vez que este é regular. Logo, teremos que há seis triângulos de lados medindo  ... onde h é a altura de um dos triângulos que compõe o Hexágono regular que coincide com sua apótema, ou seja,
... onde h é a altura de um dos triângulos que compõe o Hexágono regular que coincide com sua apótema, ou seja,  ... Logo a área de um dos triângulos será
... Logo a área de um dos triângulos será  ... Portanto a área do Hexágono será
... Portanto a área do Hexágono será
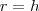 .
. ) mede
) mede  da altura do Triângulo (
da altura do Triângulo (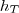 ), ou seja,
), ou seja, 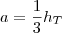 (essa é uma propriedade dos triângulos equiláteros onde o Ortocentro coincide com o Baricentro). Mas o raio da circunferência mede
(essa é uma propriedade dos triângulos equiláteros onde o Ortocentro coincide com o Baricentro). Mas o raio da circunferência mede  da altura do Triângulo equilátero dado, ou seja,
da altura do Triângulo equilátero dado, ou seja,  .
. .
. , temos que a área é
, temos que a área é 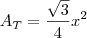 .
.

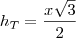 , obtemos a seguinte igualdade:
, obtemos a seguinte igualdade: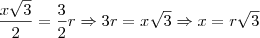
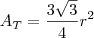
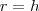 (lá do início) e
(lá do início) e 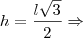 , temos
, temos 
 , então
, então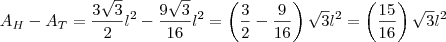
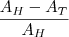 , temos
, temos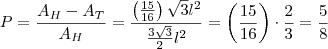



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

