 por josimar » Qua Jul 04, 2012 10:13
por josimar » Qua Jul 04, 2012 10:13
bom dia pessoal queria uma ajuda em relação ao problema abaixo
Uma urna contêm 10 bolas amarelas e n bolas vermelhas, todas elas do mesmo tamanho, mesmo peso, etc., ou seja, iguais, com exceção das cores. Um professor informa que a probabilidade de um aluno retirar, por mero acaso, uma bola da urna de cor vermelha é de 80%. Nesse sentido, qual o número de bolas vermelhas?
nesta questão acima entendi que o numero de bolas vermelhas seria 80, mas a resposta é 40 queria uma explicação sobre o problema

-
josimar
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 04, 2012 10:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: analista de sistemas
- Andamento: cursando
 por e8group » Qua Jul 04, 2012 15:32
por e8group » Qua Jul 04, 2012 15:32
Minha ideia foi essa ;
josimar escreveu:Uma urna contêm 10 bolas amarelas e n bolas vermelhas
Urna = { bola vermelha , bola amarela} , logo o número total de elementos da urna é expresso por

josimar escreveu:Um professor informa que a probabilidade de um aluno retirar, por mero acaso, uma bola da urna de cor vermelha é de 80%.
Então

ou seja ,

. Tente concluir a parti daí ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por josimar » Qui Jul 05, 2012 09:52
por josimar » Qui Jul 05, 2012 09:52
agradeço a sua ajuda, mas realmente não consegui entender, pela dedução entendo que 80 % de chances sobre a bola de uma unica cor, quer dizer que existe 80 sobre o espaço amostral de n, preciso urgente dessa resposta é questão de uma prova, foi uma prova que fiz a distancia e se a resposta que me deram estive errada, pretendo entrar com um pedido de revisão de prova, para não ter que pagar novamente essa disciplina, aguardo retorno.

-
josimar
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 04, 2012 10:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: analista de sistemas
- Andamento: cursando
 por e8group » Qui Jul 05, 2012 10:06
por e8group » Qui Jul 05, 2012 10:06
josimar escreveu:agradeço a sua ajuda, mas realmente não consegui entender, pela dedução entendo que 80 % de chances sobre a bola de uma unica cor, quer dizer que existe 80 sobre o espaço amostral de n, preciso urgente dessa resposta é questão de uma prova, foi uma prova que fiz a distancia e se a resposta que me deram estive errada, pretendo entrar com um pedido de revisão de prova, para não ter que pagar novamente essa disciplina, aguardo retorno.
Desculpe escrevi errado ..vamos lá .
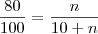
ou seja , n = 40 .
Consegue entender ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por josimar » Qui Jul 05, 2012 10:19
por josimar » Qui Jul 05, 2012 10:19
realmente voce ajudou muito obrigado

-
josimar
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 04, 2012 10:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: analista de sistemas
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida de probabilidade
por juniorufv » Sex Fev 12, 2010 12:05
- 2 Respostas
- 4651 Exibições
- Última mensagem por juniorufv

Sáb Fev 13, 2010 16:45
Estatística
-
- Dúvida Probabilidade
 por RJ1572 » Qui Mar 04, 2010 15:59
por RJ1572 » Qui Mar 04, 2010 15:59
- 1 Respostas
- 1751 Exibições
- Última mensagem por Lucio Carvalho

Qui Mar 04, 2010 17:47
Estatística
-
- Dúvida probabilidade
por RJ1572 » Seg Mai 03, 2010 15:24
- 2 Respostas
- 5530 Exibições
- Última mensagem por marcelorenato

Qui Ago 12, 2010 19:05
Estatística
-
- duvida de probabilidade
por natanskt » Ter Dez 14, 2010 21:05
- 3 Respostas
- 5408 Exibições
- Última mensagem por 0 kelvin

Qua Dez 15, 2010 22:04
Estatística
-
- Dúvida de Probabilidade
por guipomper » Dom Mar 06, 2011 18:41
- 0 Respostas
- 1165 Exibições
- Última mensagem por guipomper

Dom Mar 06, 2011 18:41
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ou seja ,
ou seja ,  . Tente concluir a parti daí ...
. Tente concluir a parti daí ...
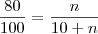 ou seja , n = 40 .
ou seja , n = 40 .