Preciso da resolução desse problema.
No livro de chamada de uma sala de aula, há alunos que vão do número 1 ao 30. De quantas maneiras podemos
escolher 3 alunos de forma que a soma de seus números de chamada seja ímpar?
R: 2030






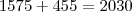

Voltar para Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



