 por samyfield » Qua Mar 27, 2013 11:45
por samyfield » Qua Mar 27, 2013 11:45
Tenho uma dificuldade a respeito deste problema: "Para cada x=0,1,2,3 ou 4, a partir de um conjunto E de pessoas, Ex corresponde ao conjunto de individuos do conjunto E que são clientes de pelo menos x operadoras de telefonia móvel e Nx, a quantidade de elementos de Ex." Considerando essas informações, julgue esta afirmação: "Para cada x do conjunto {0,1,2,3,4}, tem-se qe N4>=Nx." Acho que conseguirei resolver esse problema se alguém puder me dizer o que significa N4?
-
samyfield
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Mar 25, 2013 13:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Psicologia
- Andamento: cursando
 por timoteo » Qua Mar 27, 2013 17:59
por timoteo » Qua Mar 27, 2013 17:59
Olá.
Caso a questão esteja na íntegra e, pelo que pude entender, n4 é número de elementos de qualquer subconjunto de E. Essa é minha interpretação, a questão não está tão clara!
É isso ai!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por samyfield » Qua Mar 27, 2013 19:22
por samyfield » Qua Mar 27, 2013 19:22
[quote="timoteo"]Olá.
Caso a questão esteja na íntegra e, pelo que pude entender, n4 é número de elementos de qualquer subconjunto de E. Essa é minha interpretação, a questão não está tão clara!
É isso ai![/quote=samyfield]
timoteo,
Obrigado pela resposta! A questão está sim na íntegra. E concordo com você que ela não está muito clara, e daí a minha dificuldade em resolvê-la. A resposta da questão é que a afirmação feita é Falsa. Ou seja, N4 não é > ou = a Nx. Mas, pegando o seu gancho, não seria mais apropriado dizer que N4 é o número de elementos de UM subconjunto de E?
-
samyfield
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Mar 25, 2013 13:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Psicologia
- Andamento: cursando
 por timoteo » Qua Mar 27, 2013 22:08
por timoteo » Qua Mar 27, 2013 22:08
Correto,
olhando agora vejo que ele considera n4 é subconjunto de x e o numero de elementos de n4 realmente não é maior que o número de elementos de nx.
Para calcular o número de elementos usa-se a fórmula:

, onde n representa o número de elementos do conjunto. Sendo assim, temos: nx =
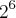
= 64, e n4 =
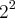
= 4. Sabendo que o vazio pertence a todo conjunto!
Espero ter ajudado!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por samyfield » Qui Mar 28, 2013 11:35
por samyfield » Qui Mar 28, 2013 11:35
timoteo escreveu:Correto,
olhando agora vejo que ele considera n4 é subconjunto de x e o numero de elementos de n4 realmente não é maior que o número de elementos de nx.
Para calcular o número de elementos usa-se a fórmula:

, onde n representa o número de elementos do conjunto. Sendo assim, temos: nx =
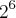
= 64, e n4 =
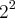
= 4. Sabendo que o vazio pertence a todo conjunto!
Espero ter ajudado!
Corretísssimo! Aqui pra nós, você está mais para professor de Matemática do que para estudante de ensino médio, conforme consta no seu perfil.
Só mais uma pequena dúvida: você calculo o nº de subconjuntos a partir de

. Chegando-se a 64 subconjuntos. Estes 64 subconjuntos
são constituídos não só dos elementos unitários como também das combinações entre eles. A pergunta é: o conjunto vazio também entra nas combinações?
Para ser mais claro: suponha um conjunto formado por [a,b, { }]. Um dos subconjuntos é [a,b]. Outro subconjunto seria também [ a, { }], ou seja, a combinação
do subconjunto [a] com o subconjunto { }?
-
samyfield
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Mar 25, 2013 13:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Psicologia
- Andamento: cursando
 por timoteo » Qui Mar 28, 2013 12:25
por timoteo » Qui Mar 28, 2013 12:25
Obrigado pelo elogio. Espero que você não esteja me estudando para alguma tese de psicologia. Rsrsrsrs...
Todos aqui são bons!
Bem, em relação a seu questionamento, sim, vocês está correta. Para mais conhecimento você deveria ver propriedades do conjunto da partes!
Espero ter ajudado!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por samyfield » Qui Mar 28, 2013 13:21
por samyfield » Qui Mar 28, 2013 13:21
timoteo escreveu:Obrigado pelo elogio. Espero que você não esteja me estudando para alguma tese de psicologia. Rsrsrsrs...
Todos aqui são bons!
Bem, em relação a seu questionamento, sim, vocês está correta. Para mais conhecimento você deveria ver propriedades do conjunto da partes!
Espero ter ajudado!
Infelizmente não! Matemática não é o meu forte. A minha área como constatou é humanas.
O objetivo do estudo é para prestar concurso público mesmo, que, entre outras, disciplinas,
inclui matemática.
Sobre a última dúvida que havia postado, encontrei a solução calculando as partes de conjuntos
formados por quantidades diferentes de elementos. Constatei que o conjunto { } só se conta como
parte unitária, sem combinação com os demais elementos.
-
samyfield
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Mar 25, 2013 13:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Psicologia
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6401 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- duvida em Conjuntos
por Fabricio dalla » Sáb Mar 05, 2011 15:32
- 4 Respostas
- 2023 Exibições
- Última mensagem por Fabricio dalla

Dom Mar 06, 2011 17:47
Álgebra Elementar
-
- Dúvida - Conjuntos
 por Mirian » Qua Mar 23, 2011 17:11
por Mirian » Qua Mar 23, 2011 17:11
- 2 Respostas
- 6980 Exibições
- Última mensagem por LuizAquino

Qui Mar 24, 2011 10:42
Álgebra Elementar
-
- duvida em conjuntos!
por janair sousa » Ter Ago 16, 2011 16:00
- 0 Respostas
- 652 Exibições
- Última mensagem por janair sousa

Ter Ago 16, 2011 16:00
Álgebra Elementar
-
- duvida em conjuntos
por bmachado » Sex Mai 18, 2012 00:20
- 3 Respostas
- 1749 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:25
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 , onde n representa o número de elementos do conjunto. Sendo assim, temos: nx =
, onde n representa o número de elementos do conjunto. Sendo assim, temos: nx = 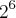 = 64, e n4 =
= 64, e n4 = 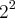 = 4. Sabendo que o vazio pertence a todo conjunto!
= 4. Sabendo que o vazio pertence a todo conjunto!
, onde n representa o número de elementos do conjunto. Sendo assim, temos: nx =
= 64, e n4 =
= 4. Sabendo que o vazio pertence a todo conjunto!
 . Chegando-se a 64 subconjuntos. Estes 64 subconjuntos
. Chegando-se a 64 subconjuntos. Estes 64 subconjuntos




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.