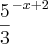 >
>  . Então:
. Então:a) S=R
b) S={x
 R/x<1}
R/x<1}c) S={x
 R/x>1}
R/x>1}d) S={x
 R/x<-1}
R/x<-1}e) S={x
 R/x>-1}
R/x>-1}
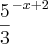 >
>  . Então:
. Então: R/x<1}
R/x<1} R/x>1}
R/x>1} R/x<-1}
R/x<-1} R/x>-1}
R/x>-1}
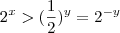 (a) .
(a) . 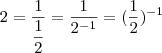 .
.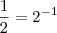 .
. real qualquer ,qual o conjunto solução para
real qualquer ,qual o conjunto solução para  da desigualdade
da desigualdade 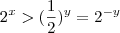 ?
?  , do ponto de vista de funções ,considerando
, do ponto de vista de funções ,considerando 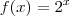 temos que
temos que  é estritamente crescente (
é estritamente crescente (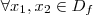 se
se  ) . Assim , dado um
) . Assim , dado um  real ,
real ,  é o conjunto solução da desigualdade .Significa que qualquer
é o conjunto solução da desigualdade .Significa que qualquer  que tomarmos no intervalo acima , satisfará a desigualdade (a) .
que tomarmos no intervalo acima , satisfará a desigualdade (a) . .Qualquer x em
.Qualquer x em 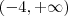 satisfaz
satisfaz 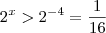 ,não é verdade ?
,não é verdade ?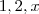 e
e  temos ,respectivamente ,
temos ,respectivamente ,  e
e  ?
? 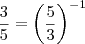 (por quê ??) e
(por quê ??) e  .Então ...
.Então ...
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.



