1.

2.
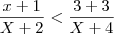
sei que é algo besta, mas não lembro como fazer...alguém poderia me ajudar?


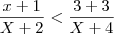

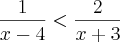


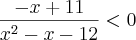

 e
e  são as raízes.
são as raízes.
Rafael16 escreveu:Olá Lenin!
Aqui tem que tirar o mmc de expressões algébricas, caso não saiba, da uma pesquisada.
Chegamos em uma inequação quociente.
Vamos chamar o numerador de f(x) e denominador de g(x). Depois achar as raízes de cada função e fazer o estudo de sinais, que é o que faremos agora:
f(x) é uma função decrescente, ou seja, para valores de x acima de 11, a função vai ser negativa, e para valores de x abaixo de 11, positiva.
Vamos agora achar a raiz da função g(x) e fazer o estudo de sinais:e
são as raízes.
g(x) é uma função com concavidade para cima, então para valores de x menor que -3, a função é positiva. Para valores de x maior que 4, a função também é positiva. E para valores de x entre -3 e 4, a função é negativa.
Depois é só fazer o jogo de sinais.
Essa é a solução
Qualquer dúvida comenta ai.
E tente fazer a 2.
 eu pegar o
eu pegar o  e fazer por inequações-produto que no caso ficaria
e fazer por inequações-produto que no caso ficaria 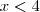 e
e  ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.
ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.
Lenin escreveu:Ah sim..vlw..outra dúvida..se aqui nessa expressãoeu pegar o
e fazer por inequações-produto que no caso ficaria
e
ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.



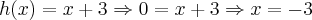

Rafael16 escreveu:Lenin escreveu:Ah sim..vlw..outra dúvida..se aqui nessa expressãoeu pegar o
e fazer por inequações-produto que no caso ficaria
e
ao invés de ir para uma equação do segundo grau e calcular delta, poderia tbm né? ou não daria o mesmo resultado em todas? Abraços.
Sim, chegaríamos no mesmo lugar. Veja:


Jogando na reta para fazer o jogo de sinais, fica:
Depois temos que fazer o jogo de sinais dessa reta com a reta do numerador.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.