


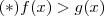 e
e 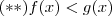 é interessante observar se
é interessante observar se  ,ou seja , se
,ou seja , se 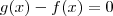 .Neste caso podemos fatorar o polinômio
.Neste caso podemos fatorar o polinômio  como produtos de polinômios . O processo de resolver as inequações (*) (**) tornam simples após a fatoração .
como produtos de polinômios . O processo de resolver as inequações (*) (**) tornam simples após a fatoração .



R0nny escreveu:Ok, é o seguinte: Supomos que a funçao f(x)= 2-x e g(x)= x²-4x+4 e dizem que querem, f(x)<g(x)... Entao o que eu estou dizendo é o seguinte eu pegar elas e junta-las, isto é,: 2-x<x²-4x+4----> -x²+4x-x-4+2----> -x²+3x-2>0
 (ou
(ou  ) de costume adicionamos em ambos membros
) de costume adicionamos em ambos membros 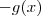 ,ficando com
,ficando com  .Assim , de forma geral, se
.Assim , de forma geral, se  é conjunto solução da desigualdade
é conjunto solução da desigualdade 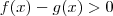 implica que para todo
implica que para todo  em
em  sempre a sentença "
sempre a sentença "  " é verdadeira .
" é verdadeira . R0nny escreveu: logo obteremos os zeros/raizes dessa equaçao: 1 e 2, sao os zeros, entao é so olhar para o sinal, como é >..... entao as chavetas serao abertas( sabendo que quando se trata de infinidade elas sempre sao abertas), logo teremos, ] - infinito, 1]U]2, + infinito[... se o sinal fosse de maior ou igual já seria diferente, as chavetas correspondentes aos zeros/raizes estariam fechadas... ] - infinito, 1]U[2, + infinito].
 .Isto porque se
.Isto porque se  é uma raiz do polinômio
é uma raiz do polinômio  ,significa que este polinômio pode ser reescrito como
,significa que este polinômio pode ser reescrito como 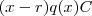 em que
em que  é um polinômio de grau :
é um polinômio de grau : 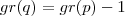 e
e  é uma constante .
é uma constante .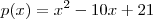 que um polinômio ou função polinomial de grau :
que um polinômio ou função polinomial de grau : 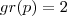 .Se peço para você desenvolver a inequação
.Se peço para você desenvolver a inequação  , da forma que a função está escrita ,digamos que é difícil resolver está desigualdade .Entretanto , se vc determinar as raízes desta função que é
, da forma que a função está escrita ,digamos que é difícil resolver está desigualdade .Entretanto , se vc determinar as raízes desta função que é  , simplesmente podemos reescrever a função
, simplesmente podemos reescrever a função  em sua forma fatorada que é
em sua forma fatorada que é  .Neste caso , para frisar a teoria proposta acima , observe que
.Neste caso , para frisar a teoria proposta acima , observe que  é um polinômio de grau :
é um polinômio de grau :  .De fato ,pela teoria ,
.De fato ,pela teoria ,  .Além disso , note que
.Além disso , note que  e
e  .Este é um exemplo que justifica que
.Este é um exemplo que justifica que 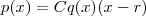 .
. é fácil determinar a solução da desigualdade
é fácil determinar a solução da desigualdade 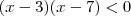 .Pois produtos de números são negativos ,sse , os números possuem sinais contrários entre-si (Veja alguns exemplos : 2(-3) < 0 , 5(-8) < 0 ... ,etc .Por outro lado , (2)(3) > 0 , (-2)(-3) > 0 , ..., etc . ) .
.Pois produtos de números são negativos ,sse , os números possuem sinais contrários entre-si (Veja alguns exemplos : 2(-3) < 0 , 5(-8) < 0 ... ,etc .Por outro lado , (2)(3) > 0 , (-2)(-3) > 0 , ..., etc . ) . 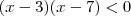 , tem-se necessariamente dois casos a considerar .
, tem-se necessariamente dois casos a considerar . e
e 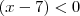
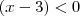 e
e 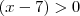 .
. R0nny escreveu:logo teremos, ] ... - infinito, 1]U]2, + infinito[... se o sinal fosse de maior ou igual já seria diferente, as chavetas correspondentes aos zeros/raizes estariam fechadas... ] - infinito, 1]U[2, + infinito]...
R0nny escreveu: A minha dúvida vem será que existe outro método de resoluçao?
R0nny escreveu:... Por exemplo, supomos que a funçao f(x)= 2x-6 e g(x)= -x²+2, e a condiçao que pedem é que: f(x)menor ou igual a g(x), como tambem g(x) maior ou igual a f(x)... Como resolveria-se com método falado por si? Chegando na resoluçao certa.




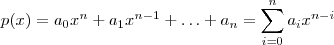 .Onde :
.Onde : 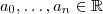 com
com 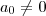 .
.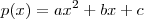 vou recomendar este site :
vou recomendar este site : 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante





