 por Thiago 86 » Ter Mar 12, 2013 07:42
por Thiago 86 » Ter Mar 12, 2013 07:42
As raizes da equação
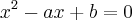
são 1 e 2. Então é verdade que:
a)

b)
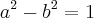
c)

d)
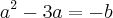
Não sei nem como me mexer para resolver essa questão.
Gostaria de saber se alguem tem um bom livro de matemática que possa me enviar para eu estudar.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Douglas16 » Ter Mar 12, 2013 11:13
por Douglas16 » Ter Mar 12, 2013 11:13
Estou respondendo com boa intenção de te ajudar.
Eu estou escrevendo um material didático para ajudar as pessoas aprenderem matemática. Por enquanto não sei se poderei disponibilizar o assunto que você quer, pois a edição do material não chegou em álgebra intermediária, estou iniciando a edição do segundo assunto de álgebra básica, que é simplificação de expressões algébricas.
Então se você quiser posso passar exercícios que te auxiliem a aprender, mas aí você escolhe se você quer que eu passe aqui no site por meio dos posts ou via e-mail, ou via Skype ou via hangout do google. Fico feliz em ter como ajudar, por isso é só deixar suas respostas aqui.
Mas tente também, se quiser, dar uma investigada no tópico de materiais do IME-USP aqui no site mesmo, lá no fim da página principal.
Então se precisar deixe mais um comentário aqui, pois também tem outras pessoas aqui do fórum que podem te ajudar, talvez estejam ocupados no momento.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Thiago 86 » Ter Mar 12, 2013 14:31
por Thiago 86 » Ter Mar 12, 2013 14:31
Obrigado pela sua atenção douglas16. Ficarei muito grato se você poder enviar os exercícios por email, pois ficaria mais fácil de eu visualizar. Sua ajuda contribuirá para a realização dos meus projetos de vida.

-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Douglas16 » Ter Mar 12, 2013 14:46
por Douglas16 » Ter Mar 12, 2013 14:46
Então, a questão é que não tenho muito tempo para digitar os exercícios, por isso se eu pudesse passar oralmente seria melhor, mas caso isso não seja possível para você, e se for importante como disse, posso fazer uma lista por dia por exemplo e te entregar ao final do dia (à noite), se Deus quiser é claro, e enviar por e-mail para você. Manda um e-mail para
323silva@gmail.com, pois é esse e-mail que vou usar para te mandar os exercícios.
Blz?
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Oi como vai...
por Fiel8 » Qua Jul 01, 2009 16:59
- 1 Respostas
- 4332 Exibições
- Última mensagem por Cleyson007

Qua Jul 01, 2009 18:11
Sistemas de Equações
-
- Sen a = 4/5 cos b = 2/3 como a < 0 e b < ?/2
por Parole » Sex Set 30, 2011 18:34
- 0 Respostas
- 3243 Exibições
- Última mensagem por Parole

Sex Set 30, 2011 18:34
Trigonometria
-
- Sen a = 4/5 cos b = 2/3 como a < 0 e b < ?/2
por Parole » Sex Set 30, 2011 18:36
- 0 Respostas
- 2780 Exibições
- Última mensagem por Parole

Sex Set 30, 2011 18:36
Trigonometria
-
- como se faz?
por Amandatkm » Ter Abr 30, 2013 17:07
- 0 Respostas
- 2704 Exibições
- Última mensagem por Amandatkm

Ter Abr 30, 2013 17:07
Equações
-
- como se faz?
por Amandatkm » Ter Abr 30, 2013 17:09
- 3 Respostas
- 2204 Exibições
- Última mensagem por Cleyson007

Qua Mai 01, 2013 13:46
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
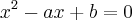 são 1 e 2. Então é verdade que:
são 1 e 2. Então é verdade que:
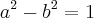

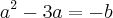

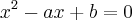 são 1 e 2. Então é verdade que:
são 1 e 2. Então é verdade que:
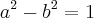

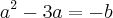





 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
