 por matheus36000 » Dom Dez 21, 2014 16:32
por matheus36000 » Dom Dez 21, 2014 16:32
Bem pessoal , estou aqui para pedir a ajuda de vocês que talvez possam me ajudar a resolver esse exercício :P
>>Essa é a equção :
![\sqrt[3]{{8}^{x}}=1 \sqrt[3]{{8}^{x}}=1](/latexrender/pictures/25fbf803b836216a07bfc3c2273d769a.png)
>>Cheguei até aqui:
![\sqrt[3]{{}^{2x}}=1 \sqrt[3]{{}^{2x}}=1](/latexrender/pictures/d868088bcaf28dd749ec41628887254f.png)
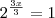
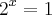
Espero que possam me ajudar a sair disso (sabendo q a resposta do ex é :0) por favor uma explicação dedidatica

-
matheus36000
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Dez 21, 2014 16:17
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Ensino Médio
- Andamento: cursando
 por Russman » Dom Dez 21, 2014 19:11
por Russman » Dom Dez 21, 2014 19:11
Está correto. De fato, x^0 = 1 para todo x Real.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matheus36000 » Dom Dez 21, 2014 20:53
por matheus36000 » Dom Dez 21, 2014 20:53
Russman escreveu:Está correto. De fato, x^0 = 1 para todo x Real.
Muito obrigado cara!! mais eu não entendo isso ... Poderia me recomendar uma citação de algum material didático explicando essa propriedade ? Obrigado

-
matheus36000
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Dez 21, 2014 16:17
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Ensino Médio
- Andamento: cursando
 por Russman » Dom Dez 21, 2014 21:14
por Russman » Dom Dez 21, 2014 21:14
Comumente, a notação

quer significar o processo de multiplicação sucessiva de um número por si mesmo. Entende-se que o número

deve ser multiplicado por si mesmo um número

de vezes.O número

é chamado de
expoente. Aqui considerando apenas o caso de expoente natural.
Daí, podemos operar este número. É verdade que

Por exemplo,

.
e também
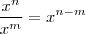
.
De acordo com essa notação se você considerar n=m então teremos o caso

.
Porém, se

então
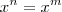
e seu quociente deve ser 1.
Este é o motivo. Apenas se quer sentido coerente à notação.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matheus36000 » Dom Dez 21, 2014 21:55
por matheus36000 » Dom Dez 21, 2014 21:55
Russman escreveu:Comumente, a notação

quer significar o processo de multiplicação sucessiva de um número por si mesmo. Entende-se que o número

deve ser multiplicado por si mesmo um número

de vezes.O número

é chamado de
expoente. Aqui considerando apenas o caso de expoente natural.
Daí, podemos operar este número. É verdade que

Por exemplo,

.
e também
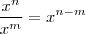
.
De acordo com essa notação se você considerar n=m então teremos o caso

.
Porém, se

então
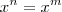
e seu quociente deve ser 1.
Este é o motivo. Apenas se quer sentido coerente à notação.
Muito Obrigado Perfeito ....
Fui eu que "marquei"
Levando em conta :
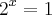
Logo :

Então :X=0
-
matheus36000
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Dez 21, 2014 16:17
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Ensino Médio
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1623 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2831 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2824 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2239 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
-
- Equação exponencial
por nan_henrique » Sáb Jul 10, 2010 13:00
- 1 Respostas
- 2188 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 13:12
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{{8}^{x}}=1 \sqrt[3]{{8}^{x}}=1](/latexrender/pictures/25fbf803b836216a07bfc3c2273d769a.png)
![\sqrt[3]{{}^{2x}}=1 \sqrt[3]{{}^{2x}}=1](/latexrender/pictures/d868088bcaf28dd749ec41628887254f.png)
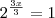
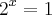


![\sqrt[3]{{8}^{x}}=1 \sqrt[3]{{8}^{x}}=1](/latexrender/pictures/25fbf803b836216a07bfc3c2273d769a.png)
![\sqrt[3]{{}^{2x}}=1 \sqrt[3]{{}^{2x}}=1](/latexrender/pictures/d868088bcaf28dd749ec41628887254f.png)
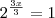
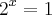





 quer significar o processo de multiplicação sucessiva de um número por si mesmo. Entende-se que o número
quer significar o processo de multiplicação sucessiva de um número por si mesmo. Entende-se que o número  deve ser multiplicado por si mesmo um número
deve ser multiplicado por si mesmo um número  de vezes.O número
de vezes.O número  é chamado de expoente. Aqui considerando apenas o caso de expoente natural.
é chamado de expoente. Aqui considerando apenas o caso de expoente natural. 
 .
.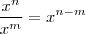 .
. .
. então
então 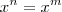 e seu quociente deve ser 1.
e seu quociente deve ser 1.
quer significar o processo de multiplicação sucessiva de um número por si mesmo. Entende-se que o número
deve ser multiplicado por si mesmo um número
de vezes.O número
é chamado de expoente. Aqui considerando apenas o caso de expoente natural.
.
.
.
então
e seu quociente deve ser 1.
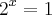


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
