>>Essa é a equção :
![\sqrt[3]{{8}^{x}}=1 \sqrt[3]{{8}^{x}}=1](/latexrender/pictures/25fbf803b836216a07bfc3c2273d769a.png)
>>Cheguei até aqui:
![\sqrt[3]{{}^{2x}}=1 \sqrt[3]{{}^{2x}}=1](/latexrender/pictures/d868088bcaf28dd749ec41628887254f.png)
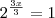
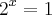
Espero que possam me ajudar a sair disso (sabendo q a resposta do ex é :0) por favor uma explicação dedidatica


![\sqrt[3]{{8}^{x}}=1 \sqrt[3]{{8}^{x}}=1](/latexrender/pictures/25fbf803b836216a07bfc3c2273d769a.png)
![\sqrt[3]{{}^{2x}}=1 \sqrt[3]{{}^{2x}}=1](/latexrender/pictures/d868088bcaf28dd749ec41628887254f.png)
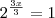
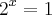



Russman escreveu:Está correto. De fato, x^0 = 1 para todo x Real.


 quer significar o processo de multiplicação sucessiva de um número por si mesmo. Entende-se que o número
quer significar o processo de multiplicação sucessiva de um número por si mesmo. Entende-se que o número  deve ser multiplicado por si mesmo um número
deve ser multiplicado por si mesmo um número  de vezes.O número
de vezes.O número  é chamado de expoente. Aqui considerando apenas o caso de expoente natural.
é chamado de expoente. Aqui considerando apenas o caso de expoente natural. 
 .
.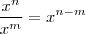 .
. .
. então
então 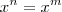 e seu quociente deve ser 1.
e seu quociente deve ser 1.
Russman escreveu:Comumente, a notaçãoquer significar o processo de multiplicação sucessiva de um número por si mesmo. Entende-se que o número
deve ser multiplicado por si mesmo um número
de vezes.O número
é chamado de expoente. Aqui considerando apenas o caso de expoente natural.
Daí, podemos operar este número. É verdade que
Por exemplo,.
e também.
De acordo com essa notação se você considerar n=m então teremos o caso.
Porém, seentão
e seu quociente deve ser 1.
Este é o motivo. Apenas se quer sentido coerente à notação.
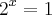


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes