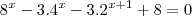
Eu tentei..
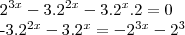
Daqui em diante eu tentei continua mas não deu certo.. alguma sugestão?
por BrunoLima » Sáb Nov 23, 2013 21:38
por e8group » Sáb Nov 23, 2013 22:50
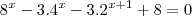
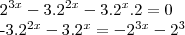
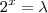,temos 
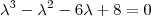.Determinando as raízes positivas desta equação ,a solução para x será 
.
por BrunoLima » Sáb Nov 23, 2013 22:58
por e8group » Sáb Nov 23, 2013 23:06
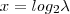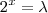teremos 
. 
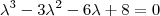é raiz desta equação . Dividindo a mesma por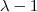 
,pode determinar as demais raízes aplicando a fórmula resolvente p/ eq. grau 2 .por e8group » Sáb Nov 23, 2013 23:21
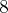. Poderia testar 
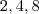,um deste números satisfaz a eq . p/ 
além do número 1 que verifiquemos .por BrunoLima » Dom Nov 24, 2013 00:00
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)