Esta equação é uma equação que degenera para

e

. Veja que se

a primeira parcela, que é

fica

que não faz sentido. Ainda se

a última parcela também degenera, pois
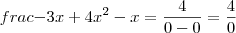
que também não faz sentido assim como pra

pois para este

que não faz sentido novamente. Logo, a equação pode admitir valores de

que sejam diferentes de

e

.
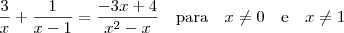
.
Para resolver a equação você deve tentar igualar todos os denominadores. O mínimo múltiplo comum entre eles é uma boa, mas eu prefiro somar as parcelas como fazemos para frações.

Logo, a equação fica
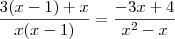

Note que

, de modo que os numeradores das frações de cada lado devem ser iguais pois os denominadores já o são. Assim,

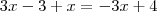




A solução

é da equação

que foi obtida simplificando
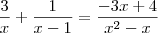
. Mas como para a eq. original excluímos

do conjunto Universo( que são os valores aceitáveis de

) o conjunto Solução da eq. original é vazio. Isto é, não existe valor de

que a satisfaça.
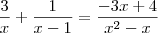
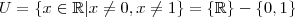
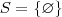



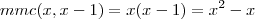





 for
for  , teremos duas divisões por zero D:
, teremos duas divisões por zero D:
 e
e  fica
fica  que não faz sentido. Ainda se
que não faz sentido. Ainda se 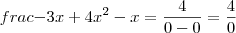 que também não faz sentido assim como pra
que também não faz sentido assim como pra  que não faz sentido novamente. Logo, a equação pode admitir valores de
que não faz sentido novamente. Logo, a equação pode admitir valores de  .
.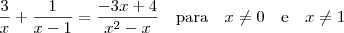 .
.
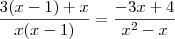

 , de modo que os numeradores das frações de cada lado devem ser iguais pois os denominadores já o são. Assim,
, de modo que os numeradores das frações de cada lado devem ser iguais pois os denominadores já o são. Assim,
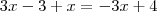



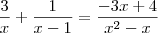 . Mas como para a eq. original excluímos
. Mas como para a eq. original excluímos 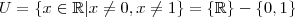
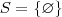



 .
.
 :
: