 por XxXMarlonXxX » Qui Out 04, 2012 16:57
por XxXMarlonXxX » Qui Out 04, 2012 16:57
Primeiramente gostaria de me apresentar, sou Marlon, sou novo por aqui e estou iniciando meus estudos para as específicas em engenharia mecânica, e como (quase) todo estudante do ensino médio tenho muitas dificuldades. Vamos a questão, depois ao que eu entendi, depois direi minha dúvida:
Admita dois números inteiros positivos, representados por a e b. Os restos das divisões de a e b por 8 são, respectivamente, 7 e 5.
Determine o resto da divisão do produto a.b por 8.
É o seguinte, as minhas conclusões (me corrijam caso eu esteja errado,por favor):
a pode ser infinitos números, mas existe uma maneira de representar, que é multiplicando o 8 por um número e somando ao resto da divisão. Chamei o este numero que multiplica de x.
a = 8.x + 7
A mesma coisa com b, chamando o número que multiplica o 8 de y:
b = 8.y + 5
Agora vamos ao produto:
a.b = (8x + 7).(8y + 5) = 64xy + 40x + 56y + 35
Aí está minha dúvida, não sei como prosseguir..
Tenho dúvidas em várias questões, meu ensino fundamental e médio foram bem abaixo da média, gostaria de contar com a ajuda de vocês.
Um abraço, obrigado!
-
XxXMarlonXxX
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qui Out 04, 2012 16:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Pré-vestibular
- Andamento: cursando
 por Cleyson007 » Qui Out 04, 2012 17:23
por Cleyson007 » Qui Out 04, 2012 17:23
Boa tarde Marlon!
Seja bem-vindo ao AjudaMatemática!
Acredito que posso ajudá-lo.. Vamos lá?
a = 8.x + 7 (OK)
b = 8.y + 5 (OK)
Quanto ao produto a.b = (8x + 7).(8y + 5) = 64xy + 40x + 56y + 35 (OK)
Chegou na beira do gol era só chutar..
64xy + 40x + 56y + 35 ---> 8(8xy + 5x +7y + 4) + 3
Chamando (8xy + 5x +7y + 4) de "q", temos: 8q + 3. Logo, o resto da divisão do produto a.b por 8 é
3Bons estudos! Qualquer dúvida estou por aqui

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por XxXMarlonXxX » Qui Out 04, 2012 17:33
por XxXMarlonXxX » Qui Out 04, 2012 17:33
Poxa, é verdade! Agora consegui enxergar, muito obrigado! Esse lance que você fez é alguma propriedade ou apenas uma jogada matemática? Pergunto isso porque, como eu disse anteriormente, meu ensino fundamental e médio foram péssimos...To tentando correr atrás do prejuízo!
Abusando ainda de sua boa vontade, você sabe de algum material, online mesmo se possível, de matemática de ensino fundamental?Pois tenho livros do ensino médio, porém as dúvidas que tenho não me dão uma "base" pra prosseguir, sempre fica umas lacunas em função de não conhecer as propriedades que não foram bem vistas no ensino fundamental...
Obrigado mais uma vez amigo, uma boa tarde!
-
XxXMarlonXxX
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qui Out 04, 2012 16:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Pré-vestibular
- Andamento: cursando
 por Cleyson007 » Qui Out 04, 2012 18:22
por Cleyson007 » Qui Out 04, 2012 18:22
Olá, boa tarde!
Marlon, fico feliz em saber que pude ajudar!
É uma propriedade matemática (ih, fugiu o nome agora..). O importante é a compreensão e saber aplicá-la.
Quanto ao material, acredito que esse site lhe seja útil:
http://www.videoaulaestudante.com/ensin ... matematicaAmigo, qualquer coisa estou por aqui

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qui Out 04, 2012 18:48
por MarceloFantini » Qui Out 04, 2012 18:48
Ele apenas aplicou a distributiva. O conceito importante aqui era notar que bastava que você escrevesse o produto como um múltiplo de 8 somado a algum resto. Como os três primeiros números eram todos múltiplos de 8, você precisava escrever 35 como um múltiplo de 8 mais algo, mas
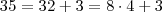
, daí usou a distributiva.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por XxXMarlonXxX » Qui Out 04, 2012 19:00
por XxXMarlonXxX » Qui Out 04, 2012 19:00
@Cleyson007
Muito obrigado mais uma vez, vou conferir o material, me ajudou bastante mesmo!
@MarceloFantini
Pois é, de início não consegui enxergar esse ponto, quando o @Cleyson007 postou a resolução eu consegui perceber, tenho de ter mais atenção mesmo...Preciso treinar mais, obrigado!
-
XxXMarlonXxX
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qui Out 04, 2012 16:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Pré-vestibular
- Andamento: cursando
 por Cleyson007 » Qui Out 04, 2012 19:40
por Cleyson007 » Qui Out 04, 2012 19:40
Boa tarde amigos!
Fantini, o nome que fugiu não é a distributiva. Para mim, esse processo de chamar de "q" e somar com o resto é que tem um nome e o nome fugiu rsrs.
Marlon, como eu te disse acredito que o site lhe será útil. Vamos fazer o seguinte: A medida que forem surgindo as dúvidas poste-as aqui no fórum, que eu, ou algum outro amigo, irá te ajudando

No mais, bons estudos!
Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qui Out 04, 2012 19:47
por MarceloFantini » Qui Out 04, 2012 19:47
Seria o algoritmo da divisão (ou algoritmo de Euclides)?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qui Out 04, 2012 19:56
por Cleyson007 » Qui Out 04, 2012 19:56
É isso ai Fantini!
Obrigado por relembrar --> Algoritmo de Euclides!
Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por XxXMarlonXxX » Qui Out 04, 2012 21:45
por XxXMarlonXxX » Qui Out 04, 2012 21:45
Distributiva eu lembro (pelo menos isso), lembro de alguns outros, que na minha época chamavam de produto notável, creio que não tenha mudado, nem foi tanto tempo assim.
Procurei sobre esse algoritmo de Euclides, é interessante pra encontrar o MDC, porém prefiro outros métodos...
@Cleyson007
Obrigado, não me falta é dúvidas! Interessante o site, só falta eu procurar uns exercícios pra complementar. Agradeço mais uma vez! Sobre as dúvidas amanhã irei postar,
um abraço a todos!
-
XxXMarlonXxX
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qui Out 04, 2012 16:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Pré-vestibular
- Andamento: cursando
 por LuizAquino » Sex Out 05, 2012 15:32
por LuizAquino » Sex Out 05, 2012 15:32
XxXMarlonXxX escreveu:(...)
Abusando ainda de sua boa vontade, você sabe de algum material, online mesmo se possível, de matemática de ensino fundamental?
(...)
Eu gostaria de recomendar as videoaulas do Nerckie:
http://www.youtube.com/nerckieSeria interessante você começar pelo curso "Matemática Zero", que faz exatamente uma revisão dos conteúdos do nível fundamental.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão UERJ
por phmarssal » Qua Nov 20, 2013 14:34
- 3 Respostas
- 2731 Exibições
- Última mensagem por Russman

Sáb Dez 07, 2013 00:25
Aritmética
-
- Questão UERJ
por phmarssal » Qua Nov 20, 2013 14:37
- 1 Respostas
- 1322 Exibições
- Última mensagem por Pessoa Estranha

Qui Nov 21, 2013 14:49
Aritmética
-
- (UERJ) - Questão de função linear
 por Levi23 » Qua Mar 11, 2009 22:28
por Levi23 » Qua Mar 11, 2009 22:28
- 1 Respostas
- 5308 Exibições
- Última mensagem por Levi23

Qua Mar 11, 2009 22:29
Funções
-
- Questão da Uerj função linear
por gustavoluiss » Seg Fev 07, 2011 22:24
- 12 Respostas
- 7774 Exibições
- Última mensagem por Santa Lucci

Ter Fev 08, 2011 01:24
Funções
-
- Questão da UERJ sobre função do 1º grau
 por kamillanjb » Qua Fev 16, 2011 19:47
por kamillanjb » Qua Fev 16, 2011 19:47
- 7 Respostas
- 6244 Exibições
- Última mensagem por kamillanjb

Dom Fev 27, 2011 20:10
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





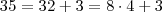 , daí usou a distributiva.
, daí usou a distributiva.
