Considere que
X = o conjunto de todos os servidores do órgão; A = o conjunto dos servidores do orgão que têm mais de 30 anos de idade;
B = o conjunto dos servidores do orgão que têm menos de 50 anos de idade e C = o conjunto dos servidores do órgão com mais de cinco anos de experiência no serviço público.
Sabendo que X, A, B, e C têm, respectivamente, 1.200, 800, 900 e 700 elementos, julgue os itens seguintes.
65 O conjunto dos servidores que satisfazem ao requisito do anúncio 1 é corretamente representado por A?B?C.
66 O conjunto de servidores que satisfazem os requisitos de apenas um anúncio é corretamente representado por
AUBUC – A?B?C.
67 X=AUB.
68 As informações do enunciado permitem inferir que, no máximo, 300 servidores não poderiam satisfazer aos requisitos de nenhum anúncio.
69 Selecionando-se ao acaso um servidor no órgão, a probabilidade de ele ter mais de 30 anos é superior a 75%.
70 Sejam p(x) e q(x) sentenças abertas com universo X dadas respectivamente por “o servidor x tem entre 30 e 50 anos de
idade” e “o servidor x possui mais de cinco anos de experiência no serviço público”. Então, se C é subconjunto de A?B, então o conjunto verdade associado à sentença aberta p(x)?q(x) coincide com o conjunto universo X.
Minha dúvida está no item 68.
Envio aqui tudo o que consegui fazer com relação a esta questão.
Primeiro fiz uma interpretação geral:


Depois fiz uma interpretação para cada anúncio:

Agora item 65:
65 O conjunto dos servidores que satisfazem ao requisito do anúncio 1 é corretamente representado por A?B?C. A foto anterior respondeu. Item correto.
Agora item 66:
Aqui cabe uma interpretação importante. Todo servidor que atender ao anúncio 1, atenderá também ao anúncio 2, pois o conjunto correspondente ao anúncio 1 está contido dentro do conjunto correspondente ao anúncio 2. Portanto, temos aqui que encontrar os servidores que satisfazem apenas ao
anúncio 2.

Por isso o item 66 é incorreto. O conjunto de servidores que satisfazem os requisitos de apenas um anúncio é corretamente representado por
(A?B)UC – A?B?C.
Agora item 67:
67 X=AUB.
Item correto. Todos os servidores ou tem mais de 30 anos ou tem menos de 50 anos.

Item 68:
Mais um pouco do que eu pensei...

Agora item 69:

Item 70:
Preciso da correção de vocês.





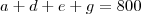
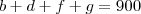
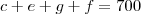
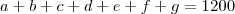
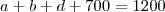


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.