Falso , não ?
Suponha que a moça nasceu em alguma data correspondente ao ano k .
Defina a relação(não é função , mas td bem ...ajudará organizar as ideias )
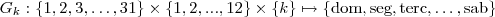
.
(
Por simplicidade (S.P.G) , vamos supor que em 1:1:k é domingo .Então temos
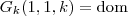
,
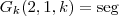
(significa 2:1:k é segunda ) ... .
Suponha ano k não bissexto (se for não problemas )
Agora forme grupos de 7 dias , escolhendo dos 7 primeiros do ano ao último . Note que ,
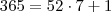
, ou seja , temos 52 grupos de 7 dias dos quais cada membro ; uma configuração da forma
(Dia do mês , Nome do mês , Ano ) , ou seja , uma tripla ordenada
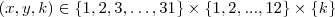
. Analisando o último grupo de 7 dias , temos que

o que implica que
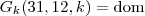
o que implica que

(aqui novo ano ) que é diferente de
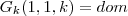
(dias da semana distinto ) , ..., aplicando o mesmo raciocínio 364 vezes vemos que
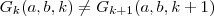
para todo

em que a configuração (Dia do mês , Nome do mês , k ) faz sentido .
O que quero dizer com isso , se a moça fizer(ou fez) niver na quarta no ano k , no ano k+1 ela comemorá na quinta que é o dia da semana de seu niver .E além disso note que k é genérico .Portanto impossível .


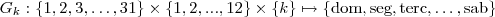 .
. 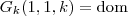 ,
, 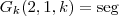 (significa 2:1:k é segunda ) ... .
(significa 2:1:k é segunda ) ... .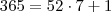 , ou seja , temos 52 grupos de 7 dias dos quais cada membro ; uma configuração da forma
, ou seja , temos 52 grupos de 7 dias dos quais cada membro ; uma configuração da forma 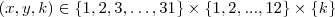 . Analisando o último grupo de 7 dias , temos que
. Analisando o último grupo de 7 dias , temos que  o que implica que
o que implica que 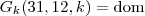 o que implica que
o que implica que  (aqui novo ano ) que é diferente de
(aqui novo ano ) que é diferente de 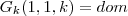 (dias da semana distinto ) , ..., aplicando o mesmo raciocínio 364 vezes vemos que
(dias da semana distinto ) , ..., aplicando o mesmo raciocínio 364 vezes vemos que 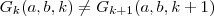 para todo
para todo  em que a configuração (Dia do mês , Nome do mês , k ) faz sentido .
em que a configuração (Dia do mês , Nome do mês , k ) faz sentido . 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.