 por TiagoFERD » Seg Dez 26, 2011 17:12
por TiagoFERD » Seg Dez 26, 2011 17:12
Boa tarde, desde já agradeço a ajuda que me deram em outro tópico,se puderem dar umas dicas nesse exercício também ficava muito agradecido..
Precisava de umas dicas para os 2, o livro explica muito sinteticamente.
Obrigado.
-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Seg Dez 26, 2011 17:55
por MarceloFantini » Seg Dez 26, 2011 17:55
A dica para o primeiro é igual a do fraol no seu outro tópico. Procure elementos que não satisfaçam as condições dadas. Veja que na primeira letra obviamente não pode ser pois uma condição para ser subespaço é que o zero pertença ao subespaço, e se a diagonal principal for não-nula não acontece.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Ter Dez 27, 2011 12:13
por LuizAquino » Ter Dez 27, 2011 12:13
Para o primeiro exercício, basta seguir as instruções de
Fantini.
Para o segundo, é só testar as três condições que caracterizam um subespaço.
Considere uma matriz

. Seja o conjunto
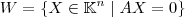
.
Para verificar se
W é subespaço de

, temos que analisar as três condições abaixo.
(i)
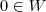
.
Essa condição é verdadeira, pois para

temos que
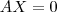
.
Obs.: note que o símbolo "0" não é o número zero, mas sim uma matriz nula de tamanho n por 1.
(ii) Se
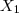
e

pertencem a
W, então

pertence a
W .
Essa condição é verdadeira, pois temos que:
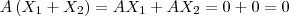
(iii) Se
X pertence a
W e

pertence a

, então

pertence a
W.
Essa condição é verdadeira, pois temos que:

Logo, como (i), (ii) e (iii) são verdadeiras, temos que
W é subespaço de

.
ObservaçãoNos seus próximos tópicos, escreva todo o texto do exercício.
Não envie o texto como uma imagem, pois isso prejudica o sistema de busca do fórum.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por TiagoFERD » Qui Dez 29, 2011 20:11
por TiagoFERD » Qui Dez 29, 2011 20:11
LuizAquino escreveu:Para o primeiro exercício, basta seguir as instruções de
Fantini.
Para o segundo, é só testar as três condições que caracterizam um subespaço.
Considere uma matriz

. Seja o conjunto
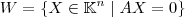
.
Para verificar se
W é subespaço de

, temos que analisar as três condições abaixo.
(i)
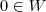
.
Essa condição é verdadeira, pois para

temos que
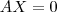
.
Obs.: note que o símbolo "0" não é o número zero, mas sim uma matriz nula de tamanho n por 1.
(ii) Se
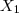
e

pertencem a
W, então

pertence a
W .
Essa condição é verdadeira, pois temos que:
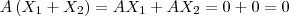
(iii) Se
X pertence a
W e

pertence a

, então

pertence a
W.
Essa condição é verdadeira, pois temos que:

Logo, como (i), (ii) e (iii) são verdadeiras, temos que
W é subespaço de

.
ObservaçãoNos seus próximos tópicos, escreva todo o texto do exercício.
Não envie o texto como uma imagem, pois isso prejudica o sistema de busca do fórum.
Boa noite LuizAquino, obrigado me ajudou muito!
-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Subespaço Vetorial] Subespaço envolvendo matrizes
por hyge » Qua Mai 02, 2018 17:04
- 2 Respostas
- 10991 Exibições
- Última mensagem por adauto martins

Dom Mai 06, 2018 12:28
Álgebra Linear
-
- [Subespaço Vetorial] Verificar que é o conjunto é subespaço
por anderson_wallace » Seg Dez 30, 2013 17:56
- 3 Respostas
- 4687 Exibições
- Última mensagem por Renato_RJ

Ter Dez 31, 2013 14:00
Álgebra Linear
-
- Demonstração de existencia de subespaço
por leandro_aur » Dom Mar 04, 2012 19:29
- 0 Respostas
- 1339 Exibições
- Última mensagem por leandro_aur

Dom Mar 04, 2012 19:29
Introdução à Álgebra Linear
-
- subespaço vetorial
 por leobcastro » Seg Jun 16, 2008 10:18
por leobcastro » Seg Jun 16, 2008 10:18
- 8 Respostas
- 26984 Exibições
- Última mensagem por Heidji

Qua Jan 27, 2010 23:16
Geometria Analítica
-
- Subespaço vetorial
por drakonifor » Qui Mar 17, 2011 16:48
- 3 Respostas
- 3990 Exibições
- Última mensagem por LuizAquino

Qui Mar 17, 2011 18:39
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 . Seja o conjunto
. Seja o conjunto 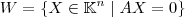 .
. , temos que analisar as três condições abaixo.
, temos que analisar as três condições abaixo.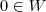 .
. temos que
temos que 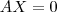 .
.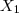 e
e  pertencem a W, então
pertencem a W, então  pertence a W .
pertence a W .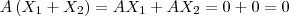
 pertence a
pertence a  , então
, então  pertence a W.
pertence a W.
 .
.
. Seja o conjunto
.
, temos que analisar as três condições abaixo.
.
temos que
.
e
pertencem a W, então
pertence a W .
pertence a
, então
pertence a W.
.
