Considere a equação x1\vec{a}+y1\vec{b}+z1\vec{c}=x2\vec{a}+y2\vec{b}+z2\vec{c}.
a)Mostre que se \vec{a}, \vec{b}, e \vec{c} são LI, então x1=x2,y1=y2 e z1=z2.
b) Mostre que se \vec{a},\vec{b} e \vec{c} são LD então não podemos concluir que x1=x2,y1=y2 e z1=z2.


 um espaço vetorial tal que
um espaço vetorial tal que 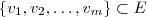 linearmente independente (L.I.) .
linearmente independente (L.I.) . 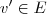 os vetores que são escritos como combinação linear de
os vetores que são escritos como combinação linear de 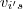 , isto é
, isto é 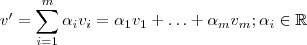 .
.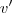 se exprimir de forma única como combinação linear dos
se exprimir de forma única como combinação linear dos 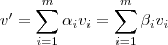 então
então  .
.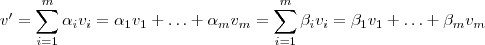 se e somente se (sse)
se e somente se (sse) 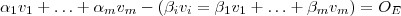 sse
sse 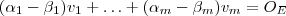 .Como
.Como 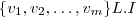 ,segue-se por definição de independência linear que todos escalares
,segue-se por definição de independência linear que todos escalares  são nulos e portanto
são nulos e portanto 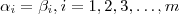 .
.
 fosse L.D. ,alguns dos escalares
fosse L.D. ,alguns dos escalares 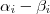 seria não nulo e com isso não podemos concluir a igualdade
seria não nulo e com isso não podemos concluir a igualdade 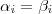 para todo
para todo 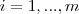 .
. ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)