W2.
por ingriddcoutinho » Dom Abr 12, 2015 19:38
W2.
por ingriddcoutinho » Seg Abr 13, 2015 20:44
por adauto martins » Ter Abr 14, 2015 12:13
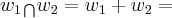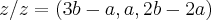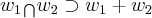
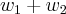eh um subespaço de 
,mas nao um subespaço gerador...![a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
[tex]a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
\begin{align}
b +& a+b & 2b-a = 0\\
2b-a & -a & -a = 0
\end{align}](/latexrender/pictures/4633d3e411d904e57929058fc5540d1b.png "a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
[tex]a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
\begin{align}
b +& a+b & 2b-a = 0\\
2b-a & -a & -a = 0
\end{align}")
por ingriddcoutinho » Ter Abr 14, 2015 13:36
por adauto martins » Ter Abr 14, 2015 15:51
={
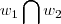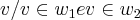}...a soluçao sera ,soluçao do sistema homogeneo,determinado pelas intersecçao das duas bases w1,w2 e q. passam pela origem(pisso sistema homogeneo),pois w1,w2 sao subespaços e devem conter a origem (0,0)logo...
por Tathiclau » Dom Dez 15, 2013 22:30
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{w}_{1}=[{u}_{1},{v}_{2}]=](/latexrender/pictures/196138ff00773385ae42492847a92089.png "{w}_{1}=[{u}_{1},{v}_{2}]=")
{
}={
}![{w}_{2}=[{u}_{2},{v}_{2}]=](/latexrender/pictures/b075d3897bbe204f1214bfc05cc050ca.png "{w}_{2}=[{u}_{2},{v}_{2}]=")
![{[tex]a{u}_{2}+b{v}_{2}](/latexrender/pictures/e8223b7e0cbbf381b32bff3c23509c0e.png "{[tex]a{u}_{2}+b{v}_{2}")
}={
}
{
}