 por ingriddcoutinho » Dom Abr 12, 2015 19:38
por ingriddcoutinho » Dom Abr 12, 2015 19:38
Dados os vetores u1=(0,1,-2), u2=(-1,0,3), v1-(1,1,1), v2=(2,-1,0) em R3, descreva os subespaços W1=[u1,v1], W2=[u2,v2] e obtenha geradores de W1

W2.
-
ingriddcoutinho
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 12, 2015 19:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por adauto martins » Seg Abr 13, 2015 18:48
por adauto martins » Seg Abr 13, 2015 18:48
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por ingriddcoutinho » Seg Abr 13, 2015 20:44
por ingriddcoutinho » Seg Abr 13, 2015 20:44
Como assim a interserçao eh a soma dos subespaços?
-
ingriddcoutinho
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 12, 2015 19:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por adauto martins » Ter Abr 14, 2015 12:13
por adauto martins » Ter Abr 14, 2015 12:13
eu escrevi errado,na verdade eh...
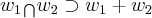
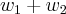
eh um subespaço de

,mas nao um subespaço gerador...
a qual se determina pelas soluçoes de...
![a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
[tex]a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
\begin{align}
b +& a+b & 2b-a = 0\\
2b-a & -a & -a = 0
\end{align} a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
[tex]a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
\begin{align}
b +& a+b & 2b-a = 0\\
2b-a & -a & -a = 0
\end{align}](/latexrender/pictures/4633d3e411d904e57929058fc5540d1b.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por ingriddcoutinho » Ter Abr 14, 2015 13:36
por ingriddcoutinho » Ter Abr 14, 2015 13:36
Não entendi nada da sua resolução, pode tentar explicar de algum outro jeito? =/
-
ingriddcoutinho
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Abr 12, 2015 19:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por adauto martins » Ter Abr 14, 2015 15:51
por adauto martins » Ter Abr 14, 2015 15:51
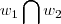
={
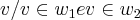
}...a soluçao sera ,soluçao do sistema homogeneo,determinado pelas intersecçao das duas bases w1,w2 e q. passam pela origem(pisso sistema homogeneo),pois w1,w2 sao subespaços e devem conter a origem (0,0)logo...
au1+bu2=0...cu2+dv2=0...a intersecçao sera a soluçao desses sistemas,onde a,b,c,d sao num.reais...em suma eh,o resto e pegar as equaçoes q. determinam as bases w1,w2 e resolver esses siastema homogeneo...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar a interseção entre os subespaços
por Cicero ferreira » Sex Mar 14, 2014 17:16
- 1 Respostas
- 1682 Exibições
- Última mensagem por Russman

Sex Mar 14, 2014 19:45
Introdução à Álgebra Linear
-
- [Subespaços vetoriais] Interseção
 por Tathiclau » Dom Dez 15, 2013 22:30
por Tathiclau » Dom Dez 15, 2013 22:30
- 1 Respostas
- 1392 Exibições
- Última mensagem por e8group

Ter Dez 17, 2013 00:16
Álgebra Linear
-
- [Álgebra Linear]-Interseção de subespaços
por Ana_Rodrigues » Ter Mai 08, 2012 23:19
- 1 Respostas
- 2317 Exibições
- Última mensagem por MarceloFantini

Qua Mai 09, 2012 21:34
Álgebra Linear
-
- [Interseção entre planos]
por sulafuly » Dom Mar 02, 2014 01:14
- 0 Respostas
- 2007 Exibições
- Última mensagem por sulafuly

Dom Mar 02, 2014 01:14
Geometria Analítica
-
- Interseção entre planos
por marinasaboia » Sex Jan 08, 2016 14:44
- 1 Respostas
- 3218 Exibições
- Última mensagem por RuuKaasu

Sex Jan 15, 2016 21:52
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 W2.
W2.

 W2.
W2.
![{w}_{1}=[{u}_{1},{v}_{2}]= {w}_{1}=[{u}_{1},{v}_{2}]=](/latexrender/pictures/196138ff00773385ae42492847a92089.png) {
{ }={
}={ }
}![{w}_{2}=[{u}_{2},{v}_{2}]= {w}_{2}=[{u}_{2},{v}_{2}]=](/latexrender/pictures/b075d3897bbe204f1214bfc05cc050ca.png)
![{[tex]a{u}_{2}+b{v}_{2} {[tex]a{u}_{2}+b{v}_{2}](/latexrender/pictures/e8223b7e0cbbf381b32bff3c23509c0e.png) }={
}={ }
}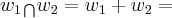 {
{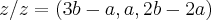 }
}

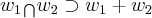
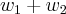 eh um subespaço de
eh um subespaço de  ,mas nao um subespaço gerador...
,mas nao um subespaço gerador...![a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
[tex]a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
\begin{align}
b +& a+b & 2b-a = 0\\
2b-a & -a & -a = 0
\end{align} a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
[tex]a{u}_{1}+b{v}_{1}=0...a{u}_{2}+b{v}_{2}=0 \Rightarrow
\begin{align}
b +& a+b & 2b-a = 0\\
2b-a & -a & -a = 0
\end{align}](/latexrender/pictures/4633d3e411d904e57929058fc5540d1b.png)


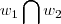 ={
={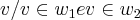 }...a soluçao sera ,soluçao do sistema homogeneo,determinado pelas intersecçao das duas bases w1,w2 e q. passam pela origem(pisso sistema homogeneo),pois w1,w2 sao subespaços e devem conter a origem (0,0)logo...
}...a soluçao sera ,soluçao do sistema homogeneo,determinado pelas intersecçao das duas bases w1,w2 e q. passam pela origem(pisso sistema homogeneo),pois w1,w2 sao subespaços e devem conter a origem (0,0)logo...





