a)encontre vetores em
 de norma 1 cujo produto interno com vetor v= (3,-1) é zero.
de norma 1 cujo produto interno com vetor v= (3,-1) é zero.b)mostre que existem infinitos vetores em
 com norma 1 e cujo produto interno com vetor v= (1,-3,5) é zero.
com norma 1 e cujo produto interno com vetor v= (1,-3,5) é zero.c)sejá u=(4,1,2), v=(0,3,8), w=(3,1,2). obtenha as expressões.
||-2u|| + 2 ||u||
||3u-5v+w||
Na primeira tentei fazer ||(x,y)||=1 e 3x-1=0
Na c) meus resultados foram
![\sqrt[]{1414} \sqrt[]{1414}](/latexrender/pictures/09ba35ced1b0beb2af921c023811eeb6.png) e
e 
![\sqrt[]{21} \sqrt[]{21}](/latexrender/pictures/35158d18eb3e07732f7dae4efebf5adb.png)


 . Para que o PI seja nulo com o vetor
. Para que o PI seja nulo com o vetor  é preciso que
é preciso que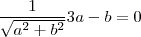
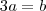 . Portanto, os vetores de R^2 normalizados perpendiculares ao vetor
. Portanto, os vetores de R^2 normalizados perpendiculares ao vetor 
 com
com  nulo gera
nulo gera
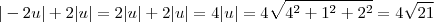
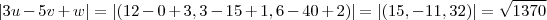

 para, por exemplo,
para, por exemplo,  . Então,
. Então,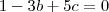
 e
e  ainda estão "amarrados" de modo que, para capturar um único vetor da forma prevista é preciso escolher duas coordenadas e calcular a terceira.
ainda estão "amarrados" de modo que, para capturar um único vetor da forma prevista é preciso escolher duas coordenadas e calcular a terceira. .
. ,
,  e para
e para  ,
,  .
.
 por
por  .
.
