 por e8group » Qui Jun 13, 2013 16:02
por e8group » Qui Jun 13, 2013 16:02
Gostaria de opiniões .Preciso concluir um exercício ,para isto preciso mostrar que para quaisquer função

em
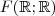
ela pode ser reescrita como
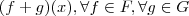
sse
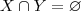
,onde
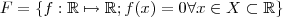
e
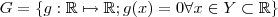
.
Primeiro ,supus (por absurdo) que
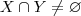
e mostrei que esta suposição é falsa para que hipótese
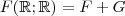
seja verdadeira . Agora preciso mostrar se
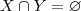
tem-se
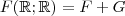
.
Posso definir
![w(x) = ([\phi +g] +[\gamma +f])(x) w(x) = ([\phi +g] +[\gamma +f])(x)](/latexrender/pictures/7afdf62dbd6bd243045fd6eb0ed12432.png)
e com isso obter que
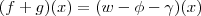
com
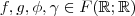
em particular
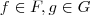
que são subespaços vetoriais de
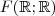
(isto foi provado no item (a) do mesmo exercício e também já foi demonstrado em outro exercício do mesmo livro que
![[tex]F(\mathbb{R};\mathbb{R}) [tex]F(\mathbb{R};\mathbb{R})](/latexrender/pictures/31caf54f8ef53fc0c2b3319fca2f82da.png)
é espaço vetorial) ??
Obrigado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Dez 15, 2013 16:06
por e8group » Dom Dez 15, 2013 16:06
Só passando pra dá um up neste tópico para ver se alguém tem alguma opinião .Este é um dos problemas que ainda não conseguir concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Espaço vetorial
por amr » Sex Abr 01, 2011 15:30
- 4 Respostas
- 8194 Exibições
- Última mensagem por Rosi7

Sáb Mai 30, 2015 00:16
Introdução à Álgebra Linear
-
- Espaço vetorial
por oliveiramerika » Sáb Jan 19, 2013 10:03
- 1 Respostas
- 5939 Exibições
- Última mensagem por young_jedi

Dom Jan 20, 2013 09:29
Álgebra Linear
-
- Espaço Vetorial
por manuel_pato1 » Sáb Mar 02, 2013 20:03
- 0 Respostas
- 1869 Exibições
- Última mensagem por manuel_pato1

Sáb Mar 02, 2013 20:03
Álgebra Linear
-
- Espaço Vetorial
por erickm93 » Qui Out 17, 2013 16:48
- 0 Respostas
- 1709 Exibições
- Última mensagem por erickm93

Qui Out 17, 2013 16:48
Álgebra Linear
-
- [Sub-espaço vetorial]
por JauM » Qua Dez 04, 2013 14:15
- 2 Respostas
- 2162 Exibições
- Última mensagem por JauM

Qui Dez 05, 2013 14:37
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 em
em 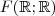 ela pode ser reescrita como
ela pode ser reescrita como 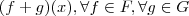 sse
sse 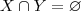 ,onde
,onde 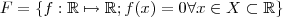 e
e 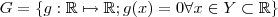 .
.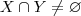 e mostrei que esta suposição é falsa para que hipótese
e mostrei que esta suposição é falsa para que hipótese 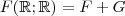 seja verdadeira . Agora preciso mostrar se
seja verdadeira . Agora preciso mostrar se 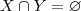 tem-se
tem-se 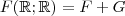 .
.![w(x) = ([\phi +g] +[\gamma +f])(x) w(x) = ([\phi +g] +[\gamma +f])(x)](/latexrender/pictures/7afdf62dbd6bd243045fd6eb0ed12432.png) e com isso obter que
e com isso obter que 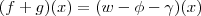 com
com 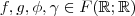 em particular
em particular 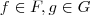 que são subespaços vetoriais de
que são subespaços vetoriais de 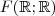 (isto foi provado no item (a) do mesmo exercício e também já foi demonstrado em outro exercício do mesmo livro que
(isto foi provado no item (a) do mesmo exercício e também já foi demonstrado em outro exercício do mesmo livro que ![[tex]F(\mathbb{R};\mathbb{R}) [tex]F(\mathbb{R};\mathbb{R})](/latexrender/pictures/31caf54f8ef53fc0c2b3319fca2f82da.png) é espaço vetorial) ??
é espaço vetorial) ??

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.