 em
em 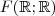 ela pode ser reescrita como
ela pode ser reescrita como 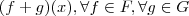 sse
sse 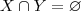 ,onde
,onde 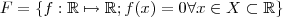 e
e 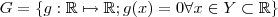 .
.Primeiro ,supus (por absurdo) que
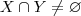 e mostrei que esta suposição é falsa para que hipótese
e mostrei que esta suposição é falsa para que hipótese 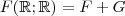 seja verdadeira . Agora preciso mostrar se
seja verdadeira . Agora preciso mostrar se 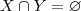 tem-se
tem-se 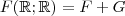 .
.Posso definir
![w(x) = ([\phi +g] +[\gamma +f])(x) w(x) = ([\phi +g] +[\gamma +f])(x)](/latexrender/pictures/7afdf62dbd6bd243045fd6eb0ed12432.png) e com isso obter que
e com isso obter que 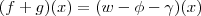 com
com 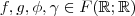 em particular
em particular 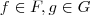 que são subespaços vetoriais de
que são subespaços vetoriais de 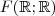 (isto foi provado no item (a) do mesmo exercício e também já foi demonstrado em outro exercício do mesmo livro que
(isto foi provado no item (a) do mesmo exercício e também já foi demonstrado em outro exercício do mesmo livro que ![[tex]F(\mathbb{R};\mathbb{R}) [tex]F(\mathbb{R};\mathbb{R})](/latexrender/pictures/31caf54f8ef53fc0c2b3319fca2f82da.png) é espaço vetorial) ??
é espaço vetorial) ??Obrigado .

